Produits scalaires
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
aloux
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Sep 2007, 18:17
-
 par aloux » 15 Mar 2008, 12:19
par aloux » 15 Mar 2008, 12:19
Bonjour a tous!
Voila j'ai un exercice sur les produits scalaires mais je n'y arrive pas...
Voila l'énoncé : On considère un triangle ABC. On pose BC=a AC=b et AB=c
On note G le centre de gravité.
montrer que AG²= 1/9( 2b²+2c²-a²)
Merci de votre aide.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 15 Mar 2008, 12:30
par Skullkid » 15 Mar 2008, 12:30
Bonjour, commence par essayer d'exprimer
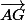
à partir de vecteurs dont tu connais la norme.
Fais aussi un dessin de la situation, ça t'aidera sûrement à y voir plus clair.
-
aloux
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Sep 2007, 18:17
-
 par aloux » 15 Mar 2008, 12:57
par aloux » 15 Mar 2008, 12:57
Quand j'exprime
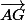
avec

,

et
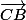
ça me donne, si je me suis pas trompé :
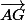
=

+
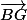
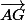
=

+
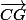
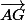
=

+
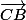
+
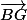
Apres je fait quoi? je remplace c, b et a par ce que j'ai trouver?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 15 Mar 2008, 13:09
par Skullkid » 15 Mar 2008, 13:09
Le problème est que tu ne connais pas plus la norme de
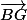
que celle de
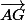
(utilise les balises [ tex] pour que ton texte soit écrit en maths).
Il te faut utiliser la définition du centre de gravité d'un triangle : c'est l'isobarycentre des 3 sommets. Ici, il est donc défini par
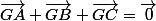
. Utilise la relation de Chasles avec le point A pour en déduire une expression de
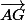
en fonction de

et

.
-
aloux
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Sep 2007, 18:17
-
 par aloux » 15 Mar 2008, 16:01
par aloux » 15 Mar 2008, 16:01
Désolé mais la, je sais pas par où aller.... Faut-il que je parte de AG²=1/9(2b²+2c²-a²) ou par exemple :

.

= 1/2(AB²+AC²-BC²)
pour ensuite arriver a AG²=1/9(2b²+2c²-a²) en remplacant AB, AC et/ou BC ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 15 Mar 2008, 16:25
par Skullkid » 15 Mar 2008, 16:25
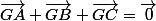
donc en "chaslant" avec A :

, c'est-à-dire
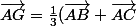)
.
D'où
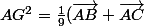^2)
. A partir de là, la formule que tu as citée,
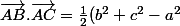)
te sera utile.
-
aloux
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Sep 2007, 18:17
-
 par aloux » 15 Mar 2008, 16:48
par aloux » 15 Mar 2008, 16:48
Ok mais quel est le lien entre
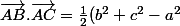)
et
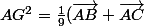^2)
?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 15 Mar 2008, 17:29
par Skullkid » 15 Mar 2008, 17:29
Il faut que tu revoies ton cours je pense...c'est une identité remarquable, de même que (a+b)² = a² + b² + 2ab,
^2=\vec{u}^2+\vec{v}^2+2\vec{u}. \vec{v})
-
aloux
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Sep 2007, 18:17
-
 par aloux » 15 Mar 2008, 17:48
par aloux » 15 Mar 2008, 17:48
J'avais vu que c'était une identité remarquable. Mais quand je développe (AB+AC)² ca me donne AB²+AC²+2ABAC, mais ensuite? Est ce que je peux remplacer AG²=AB²+AC²+2ABAC dans 1/2(AC²+AB²-BC²)?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 15 Mar 2008, 18:03
par Skullkid » 15 Mar 2008, 18:03
Ce que tu veux calculer c'est AG² pour montrer qu'il est égal à
)
. Or on a vu que
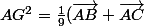^2=\frac19(c^2+b^2+2\vec{AB}. \vec{AC}))
.
Comme tu connais l'expression de

en fonction de a, b et c, le problème est réglé.
-
aloux
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Sep 2007, 18:17
-
 par aloux » 16 Mar 2008, 10:58
par aloux » 16 Mar 2008, 10:58
OK merci beaucoup et désolé si j'ai posé des questions un peu bête on va dire.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
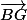 que celle de
que celle de 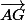 (utilise les balises [ tex] pour que ton texte soit écrit en maths).
(utilise les balises [ tex] pour que ton texte soit écrit en maths).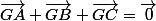 . Utilise la relation de Chasles avec le point A pour en déduire une expression de
. Utilise la relation de Chasles avec le point A pour en déduire une expression de 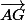 en fonction de
en fonction de  et
et  .
.