DM 1ère S - Produits Scalaires

par **Anonyme** » 14 Avr 2008, 15:25

Bonjour à tous ,
Alors voilà j'ai un DM pour la rentrée et il ya quelques question ou je n'arrive pas à répondre .... Merci d'avance de bien vouloir m'aider :we:

Exercice 5:
Calculer vecAB.vecAC dans chacun des cas suivants , en choisissant la méthode la mieux adaptée.

d. Voilà la figure :
[img][IMG]http://img224.imageshack.us/img224/6991/figuremathsyj0.th.png[/img][/IMG]

J'ai essayé avec la méthode de l'angle , vecAB.vecAC = llABllxllACllxcos(AB;AC) mais je n'y arrive pas :hein:

Exercice 4:
3) Déterminer la valeur exacte de l'angle géométrique AÔB dans les cas suivants :
a) OA=4 ; OB=8 et vecOA.OB= -16
etc etc ...
Je n'ai jamais fais ca en cours alors je vois pas du tout comment faire !

Exercice 3
Soient ABCD un carré , I le milieu de [AB] et J le milieu de [BC].
Démontrer que les droites (DI) et (AJ) sont orthogonales de deux facons :
a) En utilisant un repère orthogonal convenablement choisi.
b) Sans utiliser de repère.

Voilà la figure :
[img][IMG]http://img380.imageshack.us/img380/2497/figuremaths2jt5.th.png[/img][/IMG]

par **fatal_error** » 14 Avr 2008, 15:57

Salut, dans l'exo 5 tu as raison, il faut bien utiliser

Ici,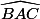

=45° , je te laisse passer en radians.

Pour le 4, même formule utilisée.

Pour le 3,
a)essaie de montrer que les triangles sont semblables et apres utilises les angles dans un des triangles.
b)Par produit scalaire bien sur!
Tu peux cherches

decompose DI et AJ en vecteurs qui vont bien.

Bonne chance!

par **Anonyme** » 16 Avr 2008, 12:14

Merci pour ta réponse !
Mais pour l'exo 5 on ne connais pas le coté AC donc je bloque et pour l'exo 3 a) j'ai pas compris ce que tu m'as dis

par **fatal_error** » 16 Avr 2008, 12:55

Re,

En fait pour la a, effectivement je n'avais pas vu qu'on ne connaissait pas AC.
En revanche, il est possible de le calculer. Tu remarques que ABC est isocèle en C. Que peux tu dire de la hauteur issue de C? Apres, c'est une application des formules cosinus ou sinus (a toi de voir :zen: )

Concernant 3,a,
je pense qu'en fait je t'ai donné une mauvaise piste, ce n'est pas la réponse qu'on attendait. Ca aurait pu marcher :
Si tu montres que ABJ et DAi sont semblables, alors on aurait facilement fait appraitre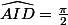

Bon, en fait à la place je pense qu'il vaut mieux prendre un graphe orthonormée, en fixant par exemple l'origine en A,et les vecteurs orthonormés du graphe tels que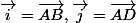

.
Ensuite, tu exprimes les cordonnées de D,I,A,J, et tu calcules

par **Anonyme** » 16 Avr 2008, 13:51

D'accord , j'y vois plus clair merci !
Je le fais et je te dis ce que j'ai trouvé :happy2:

par **Anonyme** » 16 Avr 2008, 20:00

Bon alors voilà ce que j'ai fais :

Exercice 3
Coordonnées de D (0;1)
_____________ I (0,5;0)
_____________ A (0;0)
_____________ J (1;0,5)
Donc coordonnées du vecteur DI(0,5;-1)
____________________ AJ(1;0,5)
=> vectDJ.AJ= (0,5x1)+(4x0,5)=2,5

Exercice 5
d) * La hauteur issue de C coupe le segment [AB] perpendiculairement et en son milieu D donc les triangles ACD et CBD sont rectangles en D.
** Dans le triangle ACD rectangle en D,
Cos CAB = AD/AC
Cos 45 = 2,5/AC AC=2,5/cos45 = 0,7cm
*** vectAB.AC=llABllxllACllxcos 45
= 5x0,7xcos45=2,5

Voilà merci de me dire si c'est juste :we:

par **fatal_error** » 16 Avr 2008, 20:07

vectDI.AJ= (0,5x1)+(4x0,5)=2,5

Normalement tu dois trouver 0 car (DJ) et (AJ) sont perpendiculaire

vectAB.AC=llABllxllACllxcos 45

Normalement tu dois trouver 2,5, car tu 'projettes' AC sur AB!Comme c'est le cas, ben les résultats sont bons :++:

par **Anonyme** » 16 Avr 2008, 20:15

Oulaaaaaaaa merci ,en effet j'ai fais des erreurs de calculs !!

par **Anonyme** » 16 Avr 2008, 20:22

Ah non ca ne fait plus 2,5 comme AC a changé , non ?
Et pour l'exercice 3 b) j'arrive pas non plus , je vois pas comment faire sans repère ; l'exercice 4 3)a) je n'y arrive toujours pas :cry:

par **fatal_error** » 16 Avr 2008, 20:25

Oui, tu dois trouver 5*2.5 normalement (ABx AD), le cerveau fatigue :help: .

Time to eat, je verrai le reste si perosnne ne répond avant!

par **Anonyme** » 16 Avr 2008, 20:28

Bah nan c'est pas Ad c'est AC !
D'accord , bon appétit :we:

par **fatal_error** » 16 Avr 2008, 21:09

Merci :zen:

Donc, oui AC donne dans les 3 et qq,
Le produit

Pour la 4, reecris la formule utilisée dans le premier exo, Pis remplaces!

Enfin pour decomposer DI et AJ, essaie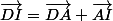

Je te laisse essayer pour AJ. L'astuce, c'est que quand tu decomposes tes vecteurs (Di et AJ), quand tu fais le produit il y ait des termes qui sautent. (par exemple

car (DA) perpendiculaire à (DC).

par **Anonyme** » 17 Avr 2008, 10:03

Ok d'accord merci !
Mais je ne comprends pas pourquoi tu as mis vectAB.vectAC= 5x 2.5 car tu viens de dire que AC fait 3 et quelques ?!

par **Anonyme** » 17 Avr 2008, 10:51

J'ai décomposé mais jvois pas ce que jdois faire après .
vect DI= vectDA+vectAI
vect AJ = (vectAI+vectIB)+BJ

Et pour l'exo 4 j'ai fais ca :
3)a. OA=4;0B=8; vectOA.vectOB=-16
vectOA.vectOB=llOAllxllOBllxcos(AOB)
-16=4x8xcos(AOB)
cos(AOB)= 32/-16=-2

Mais jcrois pas que c'est bon :hein:

par **fatal_error** » 17 Avr 2008, 11:09

Ben, ta decomposition est bonne, maintenant developpes ton produit
DI.AJ=(...).(...). Tu dois trouver 0.

Pour la 3°)a,
effectivement c'est pas bon, -1<=cos(x)<=1 donc si tu trouves -2 ya une erreur :we: .
Revoie le calcul.

Concernant le produit AB.AC:
Tu as

ce que tu as fait, mais on a aussi (c'est pareil)

car D est le projeté orthogonal de C sur (AB)

par **Anonyme** » 17 Avr 2008, 11:31

D'accord merci mais j'arrive pas à le faire , je bloque !
Oui en effet j'me suis trompé j'ai trouvé mon erreur , voilà ce que j'ai fais maintenant :
cos AOB = -16/32=0,5
<=> cos^-1(0,5)= 120° donc 2/3 PI radians

Ah d'accord pour AB.AC , j'ai compris , merci !

par **fatal_error** » 17 Avr 2008, 11:32

Ecris ce que tu as fait pour les vecteurs.

Sinon pour la solution de 120°, il y en a une autre. N'oublie pas cos(x)=cos(-x)

par **Anonyme** » 17 Avr 2008, 15:04

Voilà ce que j'ai fais pour les vecteurs :
DI.AJ=(llDAll+llAJll)x(llAIll+llIBll+llBJll)
=(DI+JI)+DA+IB-JI=DA+BJ-AB
=-2JI+DI+2DA+IB+BJ-AB
= -3IJ+IJ+DB
=-2JJ+DB
= 0

Une petite question bete , parce que j'ai un trou !
Exercice 4 :
1) On a u=2i-3j et v=-5i=2j. Calculer u.v puis llull , llvll et llu+vll.

Quand je dois calculer llull , ca donne u non ?
llull=u=2I-3j ??

Merci

par **fatal_error** » 17 Avr 2008, 15:26

attention:

DI.AJ=(llDAll+llAJll)x(llAIll+llIBll+llBJll)

D'une part la premiere parenthèse est fausse : DA+AI
D'autre part, DI.AJ est un produit scalaire l'écriture correcte est la suivante :

Ce que tu as écrit c'est la norme : autrement dit un scalaire. Dans le produit scalaire on a des vecteurs et au final seulement on obtient le scalaire.
Je te developpes DA, tu concluras pour AI.

Concernant la quatre, ben non,

A gauche un scalaire, a droite un vecteur.
La facon de calculer la norme d'un vecteur doit certainement etre écrite dans ton cours!

par **Anonyme** » 17 Avr 2008, 15:34

Ok d'accord merci , je le fais et je te montre après .
Pour la norme , je trouve pas dans mon cours et en fait d'habitude le prof nous donne llull , llvll et llu+vll et nous on doit calculer u.v a l'aide de la formule 1/2(llu+vll^2-llull^2-llvll^2) c'est pour sa que je n'y arrive pas

DM 1ère S - Produits Scalaires

DM 1ère S - Produits Scalaires

A

Qui est en ligne