Bonjour, j'ai deux problèmes d'optimisation du même type à résoudre mais je n'arrive pas à voir comment utiliser les vitesses évoquées dans l'énoncé... Je crois qu'il faut utiliser Pythagore pour trouver l'expression de la distance.
1. Deux rues se coupent à angle droit en un point P. L'une a la direction nord-sud, l'autre la direction est-ouest. Une voiture venant de l'ouest passe en P à 10h, à la vitesse constante de 20 km/h. Au même moment, une autre voiture, située à 2 km au nord du croisement, se dirige vers le sud à 50 km/h. A quel moment ces deux voitures sont-elles les plus proches l'une de l'autre? Quelle est cette distance? (R : 10h1, 7 min à 0,74 km)
2. Le passager d'un barque située à 2 km du point le plus proche de la rive désire atteindre la plus rapidement possible la maison située au bord de l'eau à 6 km en aval. Etant donné que cette personne se déplace à 3 km/h à la rame et à 5 km/h à pied, en quel point de la rive doit-il accoster pour arriver au plus vite?
(R : à 4,5 km)
Merci d'avance à ceux qui pourront m'aider! :we:
Problème d'optimisation
4 messages
- Page 1 sur 1
Bonjour,
commence par exprimer le critère en fonction des paramètres (temps, vitesses, positions), ensuite tu dérive la fonction que tu obtient.
Les racines de la dérivés (là où la dérivé s'annule) sont de bon candidat pour donner les valeurs optimal de l'objectif.
Tu peut parfois utiliser le carré du critère qui atteint son maximum dans les mêmes conditions que le critère.
commence par exprimer le critère en fonction des paramètres (temps, vitesses, positions), ensuite tu dérive la fonction que tu obtient.
Les racines de la dérivés (là où la dérivé s'annule) sont de bon candidat pour donner les valeurs optimal de l'objectif.
Tu peut parfois utiliser le carré du critère qui atteint son maximum dans les mêmes conditions que le critère.
Peut-être leur donner des coordonnées.
Le point P(0,0)
Le véhicule A est sur l'axe des x (20T ; 0)
T étant le temps. = 10h
= 10h
Le véhicule B est sur l'axe des y ( 0 : 2 - 50T). Car il est à deux kilomètres au nord et qu'il descend de 50 km chaque heure.
La distance entre deux poins c'est je crois^2+(y_B-y_A)^2})
Tu as donc la fonction qui te donne ta distance et qui varie en fonction de T. Remplace dans la formule, fais la dérivée, et voilà bonne chance!
bonne chance!
Tu vas devoir trouver un minimum pour une certaine valeur de T. Après tu remplaces dans le calcul de la distance par le temps trouvé pour obtenir la distance. Et pour avoir l'heure exacte tu ne dois pas oublier d'additionner T avec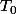
Le point P(0,0)
Le véhicule A est sur l'axe des x (20T ; 0)
T étant le temps.
Le véhicule B est sur l'axe des y ( 0 : 2 - 50T). Car il est à deux kilomètres au nord et qu'il descend de 50 km chaque heure.
La distance entre deux poins c'est je crois
Tu as donc la fonction qui te donne ta distance et qui varie en fonction de T. Remplace dans la formule, fais la dérivée, et voilà
Tu vas devoir trouver un minimum pour une certaine valeur de T. Après tu remplaces dans le calcul de la distance par le temps trouvé pour obtenir la distance. Et pour avoir l'heure exacte tu ne dois pas oublier d'additionner T avec
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
