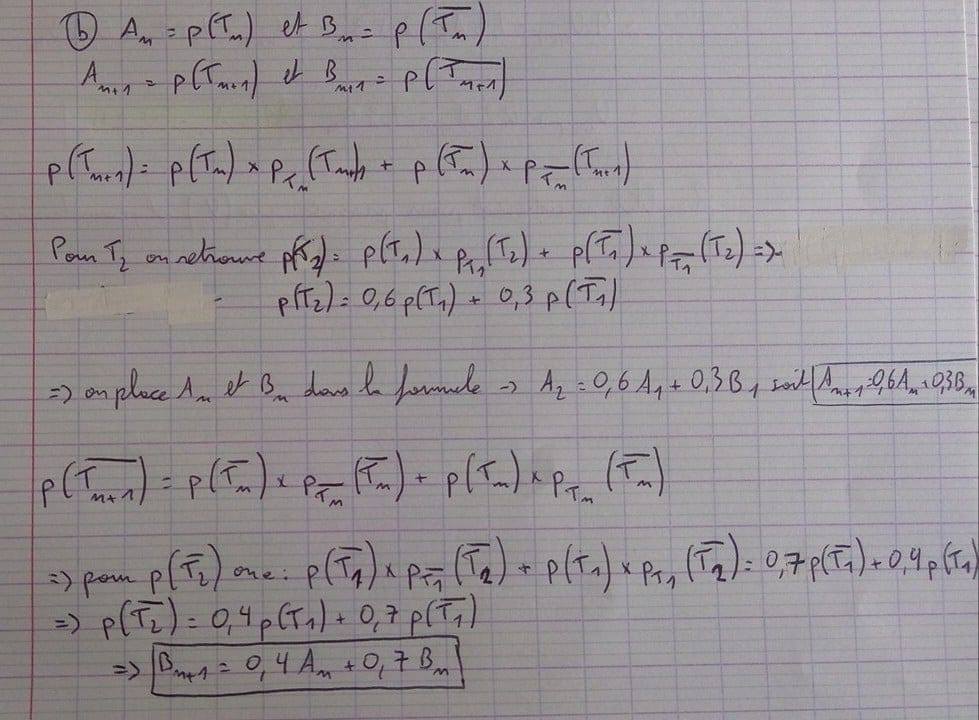Bonjour,
merci pour ton message bien clair et construit.
Effectivement, la question 1.b n'est pas traitée
En partant de la formule des probabilités totales que tu as écrite :
 = ...)
tu peux remplacer
)
par

et la proba de l'évènement contraire par

Le point clé à remarquer, c'est que la probabilité de
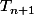
sachant

ne dépend pas de la valeur de l'entier n : c'est toujours 0.6 ! On parle de propriété de Markov.
Pour la question 2.a., pour montrer que u_n est constante, c'est la bonne idée mais pour être tout à fait rigoureux il faudrait le rédiger avec un raisonnement par récurrence
Pour montrer que
)
est géométrique, il faut trouver une relation du type
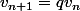
Pour cela, procède comme pour (u_n) : n'utilise que

et

(je te rappelle que
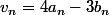
), surtout pas

cela va compliquer les calculs inutilement
Pour prendre un peu de recul : les suites (u_n) et (v_n) ne sont que des intermédiaires de calcul qui ne représentent rien concrètement, mais servent à calculer explicitement en fonction de n les quantités a_n et b_n.
Si tu connais les matrices carrées 2x2, on pourrait procéder un peu différemment pour obtenir le même résultat (calcul de la puissance n-ième d'une matrice carrée 2x2)