Primitive
Ok, merci bcp
Désolé de vous embeté encore, mais quel est le raisonement qu'il faut suivre pour trouver que la primitive de e^(ax+b) est (1/a).e^(ax+b) ?
Parceque la je marche surtout a l'intuition... je vois bien que si je dérive (1/a).e^(ax+b) j'obtient e^(ax+b), mais comment faire pour allé dans "l'autre sens"?
Désolé de vous embeté encore, mais quel est le raisonement qu'il faut suivre pour trouver que la primitive de e^(ax+b) est (1/a).e^(ax+b) ?
Parceque la je marche surtout a l'intuition... je vois bien que si je dérive (1/a).e^(ax+b) j'obtient e^(ax+b), mais comment faire pour allé dans "l'autre sens"?
Merci encore,
c'est plus clair.
Donc en fait pour résumer, si je comprend bien, pour trouver une primitive, il faut essayé de faire "apparaitre" une dérivée connue, afin de se retrouver avec une forme dont on connai la primitive, c'est a peu pres ça?
Et sinon, j'aimerais savoir si calculer une integrale indéfinie d'une fonction ça revien a trouver une primitive de cette fonction? a priorie oui, n'est ce pas?
Et enfin derniere question (pour le moment :briques: ^^) peut ont, a l'interieur d'une integrale, faire les "arrangements" que l'on veut?
par exemple, est ce que integrale de (x²+1)x, c'est la meme chose que intégrale de (x^3+x) ?
c'est plus clair.
Donc en fait pour résumer, si je comprend bien, pour trouver une primitive, il faut essayé de faire "apparaitre" une dérivée connue, afin de se retrouver avec une forme dont on connai la primitive, c'est a peu pres ça?
Et sinon, j'aimerais savoir si calculer une integrale indéfinie d'une fonction ça revien a trouver une primitive de cette fonction? a priorie oui, n'est ce pas?
Et enfin derniere question (pour le moment :briques: ^^) peut ont, a l'interieur d'une integrale, faire les "arrangements" que l'on veut?
par exemple, est ce que integrale de (x²+1)x, c'est la meme chose que intégrale de (x^3+x) ?
Merci
Voici la définition que j'ai trouver dans un vieu cahier de math:
Intégrale f(x).dx = F(x) tel que F'(x)= f(x).
Donc F(x) est la primitive de f(x), ce qui implique que:
dF(x)/dx=f(x)
Donc
dF(x)= f(x).dx
Donc
F(x) = intégrale f(x).dx
C'est une intégrale indéfinie (sans borne)
Par opposition aux intégrales définies telles que:
Intégrale (a,b) f(x).dx = F(b) - F(a).
Voila donc ma question c'etait juste pour savoir si a la question: "calculez les intégrales indéfinies suivantes" c'etait la meme chose que trouver une primitive (est ce le cas?)
Voici la définition que j'ai trouver dans un vieu cahier de math:
Intégrale f(x).dx = F(x) tel que F'(x)= f(x).
Donc F(x) est la primitive de f(x), ce qui implique que:
dF(x)/dx=f(x)
Donc
dF(x)= f(x).dx
Donc
F(x) = intégrale f(x).dx
C'est une intégrale indéfinie (sans borne)
Par opposition aux intégrales définies telles que:
Intégrale (a,b) f(x).dx = F(b) - F(a).
Voila donc ma question c'etait juste pour savoir si a la question: "calculez les intégrales indéfinies suivantes" c'etait la meme chose que trouver une primitive (est ce le cas?)
Bah sauf erreurs, calculer une intégrale sans bornes d'une fonction revient à trouver la forme générale des primitives de cette fonction.
Exemple :
=\int xdx =\frac{x^2}{2}+K) avec
avec 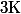 une constante.
une constante.
Il y a donc une infinité de primitives sauf si tu fixes une condition initiale, par exemple=0) donnera
donnera  .
.
Ainsi, on a trouvé l'unique primitive de vérifiant
vérifiant =0)
Thomas G :zen:
Exemple :
Il y a donc une infinité de primitives sauf si tu fixes une condition initiale, par exemple
Ainsi, on a trouvé l'unique primitive de
Thomas G :zen:
Bonsoir
Plusieurs choses :
Pour les primitives de x->exp(ax+b), des solutions ont été donné ici
Ensuite, la notationdx) est conventionnelle mais dangeureuse, car en effet elle indique une primitivation avec un opérateur d'intégration, or les conditions pour qu'une fonction soit primitivable ou intégrable ne sont pas les même, et il reste aussi bien sûr le soucis de l'ajout des constantes qui devient plus "compliqué" lorsqu'on primitive sur un ensemble disconnexe
est conventionnelle mais dangeureuse, car en effet elle indique une primitivation avec un opérateur d'intégration, or les conditions pour qu'une fonction soit primitivable ou intégrable ne sont pas les même, et il reste aussi bien sûr le soucis de l'ajout des constantes qui devient plus "compliqué" lorsqu'on primitive sur un ensemble disconnexe
D'autre part, Alexoo, comme je l'ai dit implicitement dans mon paragraphe ci dessus, une fonction peut admettre une infinité de primitive, parler de "la" primitive d'une fonction sans imposer de condition est incorrect. De plus f(x) et F(x) ne sont pas des fonctions mais des nombres, attention aux abus de langage.
Plusieurs choses :
Pour les primitives de x->exp(ax+b), des solutions ont été donné ici
Ensuite, la notation
D'autre part, Alexoo, comme je l'ai dit implicitement dans mon paragraphe ci dessus, une fonction peut admettre une infinité de primitive, parler de "la" primitive d'une fonction sans imposer de condition est incorrect. De plus f(x) et F(x) ne sont pas des fonctions mais des nombres, attention aux abus de langage.
Plusieurs choses, encore sur la rigueur (désolé, je dois surment paraitre lourd à te reprendre tout le temps, mais crois moi ce n'est pas contre toi, c'est juste qu'en maths la rigueur est une chose essentielle)
On dira plutot x^n.ln(x)dx pour préciser la variable de primitivation
On écria u'(x)=x^n et v(x)=ln(x) car u' et v sont des fonctions alors que x^n et ln(x) sont des nombres, comme je l'ai déjà dit :happy3:
Bref, outre ce pinaillage, l'idée est bonne. On sait qu'en dérivant ln, on va se retrouver avec une puissance de x (1/x plus précisément) ce qui va nous permettre d'intégrer facilement puisqu'on aura soit un polynôme, soit une fonction inverse, vu que l'autre facteur est une puissance de x.
Donc comme tu l'as fait on pose u'(x)=x^n et v(x)=ln(x). Que vallent alors u(x) et v'(x) ?
Or tu sais que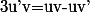
Continue
:happy3:
alexooo a écrit:Calculer l'intégrale non définie de x^n.ln(x)
On dira plutot x^n.ln(x)dx pour préciser la variable de primitivation
alexooo a écrit:u' = x^n et v= ln(x)
On écria u'(x)=x^n et v(x)=ln(x) car u' et v sont des fonctions alors que x^n et ln(x) sont des nombres, comme je l'ai déjà dit :happy3:
Bref, outre ce pinaillage, l'idée est bonne. On sait qu'en dérivant ln, on va se retrouver avec une puissance de x (1/x plus précisément) ce qui va nous permettre d'intégrer facilement puisqu'on aura soit un polynôme, soit une fonction inverse, vu que l'autre facteur est une puissance de x.
Donc comme tu l'as fait on pose u'(x)=x^n et v(x)=ln(x). Que vallent alors u(x) et v'(x) ?
Or tu sais que
Continue
:happy3:
Nightmare a écrit:Dernière remarque je pense
Là encore, sauf pour les physiciens, ce passage est incorrect, car dF(x)/dx n'est pas une réelle division, elle indique juste qu'on dérive F par rapport à la variable x.
Effectivement c'est dans un cahier de biophysique que je trouve cette définition, mais bon je suppose qu'on s'est compris c'est l'essentiel.
Cependant la ou je te suis pas c'est quand tu dis que f(x) et F(x) sont des nombres... pourquoi?
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
