bonjour,
j'ai l'enoncé d'un exercice et sa solution mais pas le dévelopement.
=> l'intégrale de e^(ax+b) = (e^(ax+b))/a + c
savez vous quelle formule d'intégration a été utilisée ?
Formule d'intégration
6 messages
- Page 1 sur 1
par nekros » 15 Juil 2006, 16:38
Salut,
Il suffit d'utiliser le fait que})'=u'(x)exp{u(x)})
Ici,=ax+b)
donc =a)
En remarquant donc que
, l'intégration devient évidente.
Thomas G :zen:
Il suffit d'utiliser le fait que
Ici,
En remarquant donc que
Thomas G :zen:
par Nightmare » 15 Juil 2006, 16:48
Bonjour :happy3:
Deux solutions :
1)Si l'on sait quedx=F(x)+C)
où F est une primitive de f :
On connait la formule de dérivation :
'=u'.e^{u})
Or :
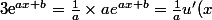e^{u(x)})
où u(x)=ax+b
Par conséquent :
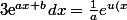}=\frac{1}{a}e^{ax+b})
2) On revient à la définition de l'intégrale :
du=\lim_{n\infty} \frac{x}{n}\Bigsum_{k=1}^{n} f(\frac{kx}{n}))
Avec
:
du=\lim_{n\to +\infty} h\Bigsum_{k=1}^{n} f(kh))
Or :
=e^{akh+b}=e^{b}e^{akh})
En sommant :
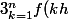=e^{b}(e^{ah}+e^{2ah}+...+e^{nah})=e^{b}\time \frac{e^{nah}-1}{e^{ah}-1})
(suite géométrique)
Ainsi :
du=\lim_{h\to 0} h\times e^{b}\times \frac{e^{nah}-1}{e^{ah}-1}=\lim_{h\to 0} (e^{ax+b}-e^{b})\times \frac{h}{e^{ah}-1}=\frac{1}{a}(e^{ax+b}-e^{b}))
:happy3:
Deux solutions :
1)Si l'on sait que
On connait la formule de dérivation :
Or :
Par conséquent :
2) On revient à la définition de l'intégrale :
Avec
Or :
En sommant :
Ainsi :
:happy3:
par nekros » 15 Juil 2006, 16:58
Pour ma part de rien.
Nigthmare, jolie pour la deuxième solution.:++:
Thomas G :zen:
Nigthmare, jolie pour la deuxième solution.:++:
Thomas G :zen:
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :