Polynomes annulateurs

[carp-sarah]

Bonjour, pouvez vous m'aider svp ??

Si A est une matrice diagonalisable, P son polynome annulateur, comment prouve ton que det(P'(A)) non nul ??

ce qu'on sait c'est que P est scindé a racines simples donc les valeurs propres de A ne sont pas racines de P'(A) et puis .. ? :S

Merci !

[Ben314]

Salut,
Déjà, une première remarque, je crois que, vu le programme actuel des lycées français, c'est plutôt une question à mettre dans le sous-forum "supérieur" ça...

Aprés, concernant ta question, si tu prend un polynôme absolument quelconque, pour calculer , le premier truc qui me vient à l'esprit, c'est de factoriser : quite à prendre les 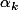(qui ne sont pas forcéments distincts) dans une cloture algébrique de ton corps de départ (par exemple dans 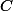si tu travaille dans ).
Tu as alors et donc (si on est en dimension ) :
où 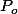est le polynôme caractéristique de
Tu en déduit que est nul ssi pour au moins un , c'est à dire ssi et ont au moins une racine commune (les racines de sont les mêmes que celle de )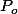

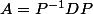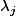Une autre façon d'obtenir le même résultat est décrie que avec diagonale, d'en déduire que donc que et tu termine en constatant que est diagonale avec les dans la diagonale si la matrice contenait les dans la diagonale. La formule que tu en déduit est cette fois :

qui, de nouveau, te dit que est nul ssi et ont au moins une racine commune.


Dans les deux cas, tu conclue en utilisant la constatation que tu a fait :

...donc les valeurs propres de A ne sont pas racines de P'...

[paquito]

Si P est scindé à racines simples, alors P est aussi le polynôme minimal de A, donc P'(A) ne peut s'annuler sinon P'(A) serait un polynôme de degré inférieur au polynôme minimal P de A qui vérifierait P'(A) =o (absurde).

[carp-sarah]

Merci !! :)

[Ben314]

Si P est scindé à racines simples, alors P est aussi le polynôme minimal de A, donc P'(A) ne peut s'annuler sinon P'(A) serait un polynôme de degré inférieur au polynôme minimal P de A qui vérifierait P'(A) =o (absurde).

Sauf que la question n'est pas de savoir si P'(A) est nul, mais de savoir si le déterminant de P'(A) est nul, et, aux dernière nouvelles, il ne me semble pas que la matrice nulle soit la seule à avoir un déterminant nul... :zen:

[paquito]

Sauf que la question n'est pas de savoir si P'(A) est nul, mais de savoir si le déterminant de P'(A) est nul, et, aux dernière nouvelles, il ne me semble pas que la matrice nulle soit la seule à avoir un déterminant nul... :zen:

Tout ce que je peux dire, c'est que si det(P'(A))=0, o est une valeur propre de P'(A) et une racine de P'(x); mais tout cela commence à dater pour moi...Bon courage.