Petite question sur les cosinus =D

[maths&co]

Bonjour à tous,

J'ai une question de maths où je bloque, pourtant je pense être assez bien partie (ou p.e pas si bien que çà !!).

La question : Calculer cos (3x) en fonction de cos (x).

Ma réponse : cos (3x)
= cos (2x+x)
= cos2x * cosx - sin2x * sinx
= (cos^2(x) - sin^2(x)) * cosx - (2sinx * cosx) (sinx)
= cos^3(x) - cosx*sin^2(x) - 2sin^2(x)*cosx*sinx

Voila et arrivée là je bloque.
Ai-je faux?

Merci de m'aider à me dépatouiller lool

[skilveg]

Salut,

Tes calculs sont corrects sauf pour la dernière ligne où tu as oublié d'enlever un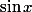 (faute d'étourderie je pense). Du coup, est-ce que tu vois comment exprimer en fonction de ?

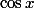Une autre manière de faire est la suivante, si tu as vu les complexes: on a ; du coup on développe, on prend la partie réelle et on aboutit là où tu étais.

[maths&co]

Ah oui merci pour l'erreur.
Oui j'ai effectivement vu les complexes, enfin je suis entrain de les faire, mais cette formule ne me dis rien.
Cependant je viens de comprendre pourquoi çà ne fonctionnait pas.
Je te remercie beaucoup.

[oscar]

Bonjoiur

Tu es bien parti
Tu dois garder UNIQUEMENT des cos x