Bonjour, la question est :
Donner la forme exponentielle du nombre complexe 3/4 + √(3)/4i.
J'ai trouvé : r=|z|=√(3)/2
Ensuite, je bloque. J'ai cherché un corrigé de mon exercice sur internet et en le regardant je suis tombé sur
3/4 + √(3)/4i = √(3)/2 * ( √(3)/2 + 1/2i )
Je suppose que ça a un lien avec z=r(cosØ+isinØ) mais je n'arrive pas à comprendre cette égalité.
Quelqu'un peut il m'aider ?
Nombre complexe
4 messages
- Page 1 sur 1
Re: nombre complexe
Salut, la méthode classique à faire ici dans les exos lycée, c'est d'exprimer  en fonction de son module :
en fonction de son module :
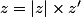 avec
avec  un nombre complexe de module 1. Le point image de z' dans le plan complexe est donc un point appartenant au cercle trigo. Son affixe est donc de la forme
un nombre complexe de module 1. Le point image de z' dans le plan complexe est donc un point appartenant au cercle trigo. Son affixe est donc de la forme 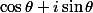 avec
avec  un argument de z' modulo 2 pi. Niveau lycee, tu peux très vite en déduire la valeur de
un argument de z' modulo 2 pi. Niveau lycee, tu peux très vite en déduire la valeur de  (qui est aussi un argument de z modulo 2 pi).
(qui est aussi un argument de z modulo 2 pi).
Re: nombre complexe
TheMoby a écrit:Bonjour, la question est :
Donner la forme exponentielle du nombre complexe 3/4 + √(3)/4i.
J'ai trouvé : r=|z|=√(3)/2
Ensuite, je bloque. J'ai cherché un corrigé de mon exercice sur internet et en le regardant je suis tombé sur
3/4 + √(3)/4i = √(3)/2 * ( √(3)/2 + 1/2i )
Je suppose que ça a un lien avec z=r(cosØ+isinØ) mais je n'arrive pas à comprendre cette égalité.
Quelqu'un peut il m'aider ?
Bonjour,
Reprenons tout !
Tout d'abord, le module d'un nombre complexe z, qui est le nombre r = |z| est en fait la distance entre l'origine du repère et le point qui représente ce complexe dans le plan orthonormé.
Si nous faisons un schéma, en plaçant le point d'affixe 3/4 + √(3)/4i, nous pouvons placer le point H qui est le projeté orthogonal sur l'axe des abscisses. Nous voyons apparaître un triangle rectangle AOH.

En d'autres termes, r s'exprime avec le théorème de Pythagore:
Donc
Maintenant comme tu le sais, nous devons calculer l'angle
Par exemple,
Donc
tu peux donc trouver cet angle AOH en utilisant la touche cos^(-1) ou bien en regardant un tableau avec des angles remarquables !
Nous pouvons faire la même chose avec le sinus de theta = coté opposé/hypoténuse, on trouverait alors
Ici, ils font en fait apparaître directement à la fois le sinus et le cosinus de l'angle theta dans la formule
Cela signifie, par identification de la partie réelle et partie imaginaire, que:
Après, la formule
Il suffit de constater sur le dessin que le point A a pour coordonnées (OH ; AH).
Or puisque cos(AOH) = OH/r, alors OH = r*cos(AOH) = r*cos(theta).
sin(AOH) = AH/r, alors AH = r*sin(AOH) = r*sin(theta)
Donc en fait, A a pour coordonnées (r*cos(theta); r*sin(theta)). Cela représente bien le complexe
r*cos(theta) + i*r* sin(theta)
= r(cos(theta) + i sin(theta))
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
