Limites

[anaël]

Bonjour à tous, est ce que quelqu'un peut m'aider?
Je bloque sur cette question:

On considère la fonction g(x)=x3/x²+3x+3 (il s'agit de x au cube au numerateur)

Montrer que g(x) s'écrit aussi sous la forme: g(x)=x-3+ (6x+9)/x²+3x+3

Determiner l'asymptote et determiner sa position.


Merci beaucoup d'avance.

[julian]

Bonjour anaël

J'ai conjecturé que g(x) admet une asymptote oblique d'équation y=x-3.
Prouvons le:
Il suffit de calculer:
Donc g(x) admet bien la droite d'équation y=x-3 comme asymptote oblique.

[anaël]

Que signifie conjecturer?

Merci

[Nightmare]

emettre une hypothése

[S@m]

Conjecturer c'est emttre une hypothese sur le resultat que tu va avoir...tu peux te dire "je supose que y=x-3 est une asymptote oblique" (dans ta tête)..C'est ce qui s'appelle une conjecture...Tu le fais souvent inconsciemment pour t'aider a toruver un resultat mais parfois il t'es demandé d'indiquer précisément tes hypothèses :id:

[julian]

Oui en effet c'est émettre une hypothèse.En fait si tu veux,on t'as demandé de prouver que
Donc je me suis dit qu'on ne t'as pas demandé çà pour faire joli et j'ai émis l'hypothèse que la droite d'équation y=x-3 était une asymptote de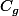 .Pourquoi?tout simplement pcq x-3 se détache de la fraction.(j'ai vérifié si c'était bien une asymptote avec ma calculatrice).
Après j'ai appliqué le fait qu'une droite D:y=ax+b est asymptote à une courbe en ou en lorsque (je te dis çà au cas où tu n'aurais pas vu çà ou tu ne t'en rappellerais pas :happy2: :id: ).
:++:

[julian]

Et j'avais oublié pour la position de l'asymptote par rapport à la courbe :id: :
tu calcules la différence f(x)-ax+b (donc ici g(x)-x+3)
-si c'est positif,l'asymptote est au-dessus de la courbe
-si c'est négatif,l'asymptote se trouve en-dessous de la courbe
:++:

[S@m]

:++: Oublie pas les parenthèses jul' :++:
C'est bien f(x)-(ax+b) :lol4: qu'i faut calculer.

Bonne continuation a toi anaël