Limites au borne de Df

[novicemaths]

Bonjour

Il y a longtemps que je n'ais pas travailler les limites, J'aurais besoin de votre aide pour un petit rappel.

Je souhaite sur cet exemple déterminer les limites au borne de Df, et déterminer les éventuelle asymptotes.

Soit la fonction f définie par

Ici, le domaine de définition de f.



Désolé, je ne me rappel plus comment mettre \ avec latex

Je dois déterminer les limites au bornes de Df, soit

Mon souci, c'est que je ne me rappel plus comment décomposer le calcul, voici mon idée.



Je sais que c'est faux, pourriez-vous me corriger svp ?

Après votre correction je ferais, en

Par avance, merci.

A +

[URemery]

Bonjour,
Petite faute dans l'ensemble de définition, les deux intervalles doivent être ouverts en 1, sinon ta fonction serait définie en 1, pas super la division par 0 Mais c'est pas le cœur du problème !

L'idée c'est de factoriser par le terme le plus fort, je m'explique :

On a factorisé par x au numérateur car c'est le terme le plus fort (celui qui va le plus vite vers ), idem pour le dénominateur.
Ainsi
Est-ce que ça t'aide à conclure ?

Même méthode pour la limite en et en pour la limite en 1, même pas besoin d'une astuce

[capitaine nuggets]

Salut !

Le "" s'écrit "\setminus" :

- En ce qui concerne la limite en , on factorise au numérateur et dénominateur par le monôme de plus haut degré (sans son coefficient) :



De façon générale, Si tu as deux fonctions polynomiales et alors :



- La courbe représentative de admet une asymptote horizontale si les limites sont finies et égales.

- Ensuite,
Il te suffit alors seulement de connaître

Pour simplifier l'étude des limites aux bornes du domaine, une idée serait par exemple de trouver deux réels tels que .

[novicemaths]

Bonjour

D'abord merci pour l'aide que vous m'apporter.

Je j'ai bien compris, on transforme en

Puis, on fait et

Donc ce qui donne un résultat

Donc, la limite de

Avant d'aller plus loin dans les calculs, je souhaite savoir, si j'ai compris.

Est ce que cette limite est de forme indéterminé ?

Pour déterminer une éventuelle asymptote, il faut faire un autre calcul ?

A bientôt

[capitaine nuggets]

Salut !

Bonjour

D'abord merci pour l'aide que vous m'apporter.

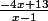
Je j'ai bien compris, on transforme en

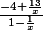
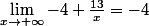
Puis, on fait et

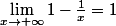
Donc ce qui donne un résultat

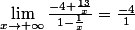
Donc, la limite de

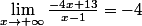
Avant d'aller plus loin dans les calculs, je souhaite savoir, si j'ai compris.

Est ce que cette limite est de forme indéterminé ?

Pour déterminer une éventuelle asymptote, il faut faire un autre calcul ?

A bientôt

Oui,

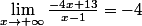
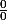
On dit qu'une limite est de forme indéterminée si lorsqu'on fait la limite du numérateur et du dénominateur, on tombe sur quelque chose de la forme ou .

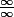
Question asymptotes, il y en a déjà deux : une verticale et une horizontale.
- L'horizontale d'équation y= -4 provient de ce que j'ai dit précédemment dans mon message précédent (il te reste néanmoins à montrer qu'on a aussi ).
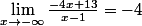
- Il y a une asymptote verticale d'équation : pour cela, il faut montrer que et .
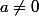
- Enfin, on dit que la courbe de admet une asymptote oblique d'équation , , si .
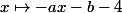
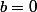
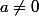
Ici, on peut voir qu'il n'y en aura pas car on a vu que donc s'il existe effectivement un telle asymptote oblique, on devrait avoir . Or la fonction est de type affine donc la seule manière d'avoir : , c'est que et . Or il faut que , donc on a une contradiction quand à l'existence d'une asymptote oblique.

[titine]

C'est tout à fait juste.
Si tu considères la limite en +inf de -4x+13 , c'est -inf.
Et la limite en +inf de x-1 est +inf.
Or inf/inf est une forme indéterminée.
Dans ces cas là il faut commencer par transformer l'expression pour ne plus avoir une forme indéterminée.
C'est pour cela que l'on transforme (-4x+13)/(x-1) en (-4+13/x)/(1-1/x). On a alors le numérateur qui a pour limite -4 et le dénominateur qui a pour limite 1.

Comme la limite en +inf de f(x) est -4, tu peux en déduire, par définition, que la courbe de f admet une tangente horizontale d'équation y=-4.

[novicemaths]

Bonjour

J'ai une dernier question.
Est-ce que on aurait pus utiliser la méthode, le théorème des termes de plus haut degré pour calculer les limites ?

A +

[anthony_unac]

Bonjour,
Absolument, et c'est tout à fait autorisé si votre prof vous l'a enseigné mais c'est très classe de lever une indétermination en transformant l'expression de départ (ça permet de faire un peu de gymnastique histoire de ne pas trop se rouiller les neurones)