Limites de suite
3 messages
- Page 1 sur 1
Limites de suite
Soit Un une suite croissante, à termes positifs et majorée par 1. Cette suite est définie par la relation de récurrence Un+1 = (2Un + 1)/(Un + 2). La limite de Un quand n tend vers + l'infini est notée l. On cherche cette limite. Dans la correction il est dit que par composition des limites, la limite de Un+1 quand n tend vers + l'infini est égale à l. Moi par composition des limites de trouve (2l + 1)/(l + 2). Je comprend que si Un tend vers l alors Un+1 aussi mais je ne comprend pas pourquoi on utilise le terme "par composition des limites. Si quelqu'un peut m'éclairer. merci d'avance.
Re: Limites de suite
Bonjour
Si la suite) a pour limite
a pour limite  il est assez clair que
il est assez clair que  tend vers
tend vers  puisque il s'agit de la même suite...
puisque il s'agit de la même suite...
Pour ce qui est de la composition si on pose telle que
telle que =n+1)
alors)
or=+\infty)
et=l)
donc par composition
=l)
Si la suite
Pour ce qui est de la composition si on pose
alors
or
et
donc par composition
Re: Limites de suite
Salut,
Pour compléter ce que dit Catamat, à mon sens, il y a deux choses qui peuvent être considérées comme étant de la "composition de limites" :
1) Tu as une suite_{n\geq 0}) qui tend vers un réel
qui tend vers un réel  et tu considère une suite de la forme
et tu considère une suite de la forme 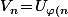}) où
où 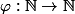 est une fonction qui tend vers
est une fonction qui tend vers  lorsque la variable tend vers
lorsque la variable tend vers  . Dans ce cas, la suite
. Dans ce cas, la suite _{n\geq 0}) tend aussi vers le réel
tend aussi vers le réel  .
.
2) Tu as une suite_{n\geq 0}) qui tend vers un réel
qui tend vers un réel  et tu considère une suite de la forme
et tu considère une suite de la forme 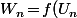) où
où  est une fonction définie au voisinage de
est une fonction définie au voisinage de  et continue en
et continue en  . Dans ce cas, la suite
. Dans ce cas, la suite _{n\geq 0}) tend vers le réel
tend vers le réel ) .
.
Et en fait, si tu regarde une suite comme une application de
de 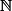 dans
dans  , dans les deux cas, on a bien composé cette application avec une deuxième application : dans le premier cas, on a composé "à droite" :
, dans les deux cas, on a bien composé cette application avec une deuxième application : dans le premier cas, on a composé "à droite" : 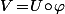 et dans le deuxième "à gauche" :
et dans le deuxième "à gauche" : 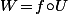
Pour compléter ce que dit Catamat, à mon sens, il y a deux choses qui peuvent être considérées comme étant de la "composition de limites" :
1) Tu as une suite
2) Tu as une suite
Et en fait, si tu regarde une suite comme une application
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
