Les Olympiades

[Benhamedi]

Chers camarades, je viens de passer un examen d'Olympiades et sincérement ce n'était pas du tout facile. Alors je voudrais bien savoir mes défaillances et la réponse de l'examen que vous trouvrez dans le lien ci-contre:

[Benhamedi]

Aucune réponse à ma question??

[pascal16]

Si je ne me trompe pas :
le cercle circonscrit à ABK a son centre sur la bissectrice de BAC. Et si on trace un cercle sur la bissectrice d'un angle, l'égalité des distances (du moment qu'il y a intersection, même multiples) AE et AF est assuré. La complexité de la construction sert juste à avoir une solution unique mais semble servir à écarter le lecteur du droit chemin

[pascal16]

pour le 3
si on décompose 2018, il faut que 1 , 2 et 1009 soit dans M
donc 2*1009+1=2019=3*673 aussi
donc 3 et 673 aussi
....
en testant quelques nombre de plus, on doit générer 1,2,3,4,5
la partie 2 doit monter que tous nombre >5 s'écrit avec des nombre 1,2,3,4,5 et la propriété "km+1"
ça sent la récurrence
si on suppose la ppté vraie jusqu'au rang n-1
n impair -> n-1 pair s'écrit 2*p or 2 et p>2 dans M par HR donc 2p+1 = n aussi
n pair-> n-1 s'écrit 3p ou 3p+2, cas 3p facile, reste le case 3p+2

[pascal16]

au passage, sans '6', on n'engendre pas N

[Benhamedi]

on peut pas dire que si 1 et 2 appartiennent à M alors leur somme (3) appartient aussi à M ????

[Ben314]

Pour l'exo 1), les 3 inéquations impliquent que :

c'est à dire où
Or, pour tout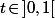 on a :

donc pour tout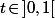 on a avec égalité ssi 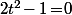c'est à dire .
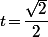L'inégalité n'est donc vérifiée que pour et il est clair que dans ce cas là, les trois inégalités de départ sont bien vérifiées.

L'exercice 2) il est totalement couillon : si on note la symétrie orthogonale par rapport à (AK) alors :
- Vu que (AK), est la bissectrice de l'angle (BAC), envoie la droite (AB) sur (AC).
- Vu que le triangle ADK est rectangle en D, son cercle circonscrit c'est celui de diamètre [AK] donc la symétrie laisse le cercle globalement invariant.
Et on en déduit évidement que s(E)=F et donc que AE=AF.

[Ben314]

on peut pas dire que si 1 et 2 appartiennent à M alors leur somme (3) appartient aussi à M ????

Un énoncé, ça se lit (et ça se comprend) et il n'y a absolument rien dans celui là qui dit que la somme de deux éléments de M est dans M.

[Ben314]

Pour l'exercice 3) :
- Comme 2018 = 2 x 1009 est dans M, (ii) => 1 , 2 et 1009 sont dans M.
- (iii) => 2x1009 + 1 = 2019 = 3 x 673 est dans M puis (ii) => 3 et 673 sont dans M.
- (iii) => 3x673 + 1 = 2020 = 4 x 505 = 5 x 404 est dans M puis (ii) => 4 et 5 sont dans M.
Montrons par récurrence que, pour tout entier , l'ensemble est contenu dans M.
Jusqu'à , c'est déjà fait.
Supposons que, pour un certain on ait .
- Si est pair alors on a avec et 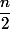dans M (par H.R.) donc (iii) est dans .
- De même, si est impair alors et sont >1, distincts et dans M donc est dans .
Puis, vu que et sont >1, distincts et dans M c'est que est aussi dans M.
Et comme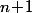 divise le (ii) nous dit que 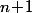est dans M.

[pascal16]

Bien vu Ben
à partir de {1;2;3;4;5}
6 s'obtient par (5*7+1)=6*6, 7 étant déjà généré par 3*2+1