Olympiades lyon 2003
49 messages
- Page 3 sur 3 - 1, 2, 3
pour ma part, j'ai la conscience tranquille :we:
j'ai écrit une démo rudimentaire qui marche dans ce cas particulier où
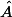 est droit
est droit
je ne suis pas convaincu que AMH soient alignés
l'étude du cas général est intéressante (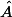 non droit)
non droit)
M est le point de Lemoine
il faudrait écrire la démo qu'il est situé à l'intersection des 3 symédianes.
j'ai écrit une démo rudimentaire qui marche dans ce cas particulier où
je ne suis pas convaincu que AMH soient alignés
l'étude du cas général est intéressante (
M est le point de Lemoine
il faudrait écrire la démo qu'il est situé à l'intersection des 3 symédianes.
mathelot a écrit:Merci Zweig pour le point de Lemoine et les symédianes (je ne connaissais pas)
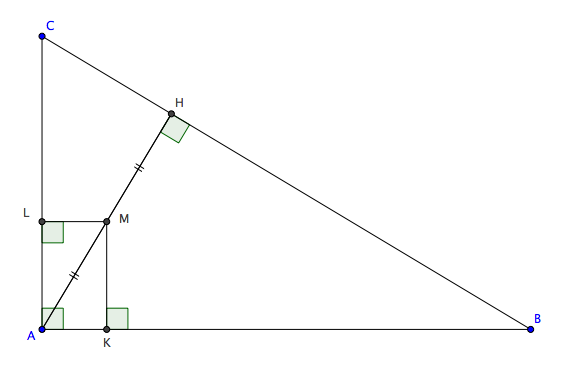
H,K,L les projetés de M sur [BC],[AB],[AC]
les airessont proportionnelles
à
elles s'écriventavec
où S est l'aire de ABC.
[MK] est une hauteur du triangle AMB d'airede base [AB] de longueur c.
la droite (CM) coupe [AB] en I.
On applique le théorème de Thalès dans le triangle ACI.
par complémentarité
M est donc barycentre deet
Soit maintenant L barycentre de
d'après ce qui précède, M=L.
remarque: ce qui est (très) ennuyeux, c'est que la démo dépend
fortement de l'angle droit en A.
Ce qui reste le point de lemoine quand même ....
Pour montrer cette propriété :
Soit ABC un triangle avec AB = c, AC = b et BC = a. Soit une symédiane issue de A, coupant (BC) et A" et M un point de celle-ci. On note K' et H' les projetés orhogonaux de M, respectivement, sur (AB) et (AC). On considère une médiane issue de A coupant (BC) en A' et M' un point de celle-ci. Soient K et H les projetés orthogonaux de M' sur, respectivement, (AB) et (AC). Alors d'après le théorème de Thalès :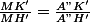 et
et 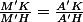 .
.
Par définition les angles géométriques (en vecteurs) (AB, AA") et (AC, AA') sont égaux, on le note . On a alors :
. On a alors :
} = \frac{A'H}{A'K})
Comme les triangles ABA' et AA'C ont des bases égales et même hauteur issue de A, alors leurs aires sont égales ; on la note S. On a :
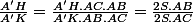
D'où,
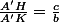
Par suite,
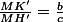
Par permutation circulaire, on montre des résultats analogues pour des points appartenant aux deux autres symédianes. Comme le point de Lemoine est le point de concours de ces symédianes, alors ces trois points variables sont confondus, d'où :
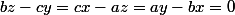 avec x, y et z les distances du point de Lemoine au côtés du triangle, d'où l'égalité désirée après divisions.
avec x, y et z les distances du point de Lemoine au côtés du triangle, d'où l'égalité désirée après divisions.
Ericovitchi a écrit:Avec x,y,z les distances de M à BC,AC et AB, en fait le problème revient à résoudre
(car l'aire AMB c'est cz et dire qu'elles sont proportionnelles c'est dire que cz/c²=by/b²=ax/a²)
J'ai pas lu le reste, mais arrivé à ce stade, on peut conclure : le seul point qui vérifie cette égalité est le point de Lemoine (intersection des symédianes) :zen:
Soit ABC un triangle avec AB = c, AC = b et BC = a. Soit une symédiane issue de A, coupant (BC) et A" et M un point de celle-ci. On note K' et H' les projetés orhogonaux de M, respectivement, sur (AB) et (AC). On considère une médiane issue de A coupant (BC) en A' et M' un point de celle-ci. Soient K et H les projetés orthogonaux de M' sur, respectivement, (AB) et (AC). Alors d'après le théorème de Thalès :
Par définition les angles géométriques (en vecteurs) (AB, AA") et (AC, AA') sont égaux, on le note
Comme les triangles ABA' et AA'C ont des bases égales et même hauteur issue de A, alors leurs aires sont égales ; on la note S. On a :
D'où,
Par suite,
Par permutation circulaire, on montre des résultats analogues pour des points appartenant aux deux autres symédianes. Comme le point de Lemoine est le point de concours de ces symédianes, alors ces trois points variables sont confondus, d'où :
49 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :