[Olympiades] Barycentre

[Anonyme]

Bonjour,

Dans mon livre de maths, dans un chapitre sur les barycentre j'ai trouve un problème d'olympiades probablement assez connu. Seulement voila j'ai réussi a résoudre ce problème sans utiliser les barycentre et je meurs d'envie de savoir comment le résoudre avec les barycentres.

Voici le problème en question:
Le lac

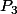
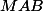
Trois propriétaires , , disposent chacun d’une parcelle de terrain carrée, jouxtant un lac triangulaire rectangle en . Ils décident de délimiter leurs "eaux territoriales" en plaçant une bouée de telle sorte que les surfaces , et soient proportionnelles aux aires des parcelles adjacentes.


Déterminer la position de cette bouée dans le lac.

Merci

[benekire2]

Au milieu de la hauteur :) Tu veut la démo ? Je l'avais fais ^^ Amusant

c'est un cas particulier ( triangle rectangle) du point de lemoine.

[benekire2]

Je connais plusieurs méthodes pour y parvenir, dont une analytique intéressante bien que pas très esthétique ( parce que analytique lol)

PS: Ah mince ma méthode n'utilise les barycentres qu'au début ... et je suppose que tu as fait pareil !!

PS2: Comment as-tu précéder ? En gros ...

[Anonyme]

J'ai montrer par les angles qu'il est sur la hauteur et après sur sa moitie.
Démonstration assez simple.

En fait j'arrive pas a traduire les donne en vecteur et donc je ne m'approche pas du barycentre.

[Nightmare]

Salut !

Aux vues de l'énoncé, on a bien envie de dire que M est le barycentre des points pondérés par les surfaces des carrés opposé. Essaye de montrer que ce barycentre correspond bien au point voulu. En considérant les hauteurs et les relations de proportionnalité sur les aires, on doit s'en sortir :happy3:

[benekire2]

Après je signale que j'avais trouver cet exercice dans le chapitre produit scalaire alors ...


En fait le problème se résume a trouver M barycentre de (A,a²);(B,b²);(C,c²) mais je t'apprend rien .

Bon en fait dans ma solution, c'est fini les barycentres... de là on projette M sur [AB] en C' et de la même manière on place A' et B'.

On doit donc respecter la condition de proportionnalité :
(0.5MC'*AB)/AB²=(0.5MB'*AC)/AC²=(0.5MA'*BC)/BC²

que l'on réécrit MC'/AB=MB'/AC=MA'/BC

( je pense que tout le monde a fait dans ce style là ... )

La on étudie nos triangles; grace a MC'/AB=MB'/AC on a
Donc MB'C' est semblable a ACB ie AB'C' semblable a ABC .
De manière évidente ABC est semblable a A'AC ie AB'C' semblable a A'AC.

PAr les angles on a M sur AA'

Enfin, pour finir comme MB'C' est semblable a ACB on a: MB'/AC=MC'/AB=B'C'/BC

que l'on réécrit :
MB'/AC=MC'/AB=AM/BC

( La j'ai réfléchis comme un con ... )

En reprenant la première égalité :

MB'/AC=MA'/BC

on obtient en remplaçant avec celle d'avant :
AM/BC=A'M/BC <=> AM=A'M

Fin de l'histoire !!

[benekire2]

J'ai montrer par les angles qu'il est sur la hauteur et après sur sa moitie.
Démonstration assez simple.

En fait j'arrive pas a traduire les donne en vecteur et donc je ne m'approche pas du barycentre.

On a donc la même ...

Salut !

Aux vues de l'énoncé, on a bien envie de dire que M est le barycentre des points pondérés par les surfaces des carrés opposé. Essaye de montrer que ce barycentre correspond bien au point voulu. En considérant les hauteurs et les relations de proportionnalité sur les aires, on doit s'en sortir

Je voit qu'on a tous la même

[Anonyme]

En effet Benekire on a la meme demo :zen:

Salut Nightmare !

Aux vues de l'énoncé, on a bien envie de dire que M est le barycentre des points pondérés par les surfaces des carrés opposé.

Pourtant sans connaitre un tel résultat d'avance il est impossible de le deviner a moins que je passe a cote de quelque chose d'évident.

Essaye de montrer que ce barycentre correspond bien au point voulu. En considérant les hauteurs et les relations de proportionnalité sur les aires, on doit s'en sortir :happy3:

Je pense avoir montrer qu'un tel point convient. Je vais vérifier ...

Mais bon supposons que je ne sais pas ce résultat d'avance. Dans ce cas comment a partir des relations de proportionnalité aire-hauteur.cote arriver a trouver qu'il s'agit bien du barycentre des point précédemment cites. La question est de trouver comment traduire ces rapport égaux en une somme de vecteur.

[benekire2]

Ben c'est un peu intuitif en fait, quand t'as une droite AB de 10 avec C placé au bout de 2 et bien C barycentre de A8 et B2 en fait tu pondère par la longueur "de l'autre coté" avec trois points c'est le même principe sauf que tu pondère par les aires opposées que tu sais proportionelles aux cotés.

C'est clair ou pas du tout ?

[Anonyme]

Ben c'est un peu intuitif en fait, quand t'as une droite AB de 10 avec C placé au bout de 2 et bien C barycentre de A8 et B2 en fait tu pondère par la longueur "de l'autre coté" avec trois points c'est le même principe sauf que tu pondère par les aires opposées que tu sais proportionelles aux cotés.

C'est clair ou pas du tout ?

Non pas vraiment :triste:

[Nightmare]

Le barycentre, c'est un centre d'inertie. On peut voir les poids qui pondèrent les points comme des masses (Edit : accrochées aux points) qui font "pencher" le triangle, en le considérant par exemple comme une plaque métallique (homogène). Si l'on rajoute 3 plaques métalliques carrées (homogènes aussi) et si l'on veut qu'il y ait inertie, il faut trouver le centre d'inertie de sorte que les masses permettent l'équilibre. Vu qu'on suppose les plaques homogènes, l'inertie dépend uniquement de leur surface et pour que le phénomène se produise, il faut bien intuitivement pondérer chaque sommet du triangle par la masse qui correspond à la surface carrée opposée.

[Anonyme]

il faut bien intuitivement pondérer chaque sommet du triangle par la masse qui correspond à la surface carrée opposée.

En faisant cela j'ai pas l'impression que je cherche a partager un triangle de tel façon que les aires des triangles formées soient proportionnelles a l'aire de leurs carres respectif.

En même temps l'intuition ne se transmet pas.

Vois tu un moyen mathematique rigoureux d'arriver a démontrer que le point recherche est le barycentre dont on parle ?

[Nightmare]

A priori, c'est ce que fait Benekire non?

[Anonyme]

A priori, c'est ce que fait Benekire non?

Il a résolu l'exo sans barycentre.

Je crois que je me suis mal exprimer : Je ne cherche pas a résoudre l'exo puis de vérifier que le point obtenu est le barycentre de
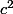Mais plutôt que dans la demo j'arrive a trouver que le point G qu'on recherche satisfait: GA+GB+GC=0 et alors je déduis que c'est le barycentre de

NB:en gras = vecteur

[benekire2]

A_1__C____2_____B

Je fais du dessin :)

Ici, Est on d'accord que C est barycentre de (A,2)(B,1) ? Oui naturellement. Tu peut le démontrer.

Tu remarque que l'on pondère par "la longueur opposée"

Maintenant avec les triangles c'est la même chose, on pondère par l'aire opposée. Techniquement ça se démontre aussi. Tu le pose en lemme, tu le démontre et tu peut ainsi affirmer que M est barycentre de (A,a²)(B,b²)(C,c²)
et après tu résous comme on a fait. Tu trouvera pas vraiment de méthode purement barycentrique je le crains ( j'ai cherché moi aussi )


Ca convient ou je te met un dessin du triangle mieux expliqué ? ?

[Ben314]

Salut,
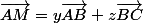
Si tu considère le barycentre M de (A,x) , (B,y), (C,z) avec x,y,z>0 et x+y+z=1 alors on a et les deux vecteurs et sont les hauteurs des triangles ABM et ACM.
Les surfaces respectives de ABM et ACM sont donc et et tu n'as plus qu'à égaliser aver les surfaces voulues pour trouver y et z (évidement, x=1-y-z)

[benekire2]

Hé salut ben !! Ca faisait un bout de temps qu'on t'avais pas vu !! ( 2 jours)
Tu fétait pi ?? :zen:

[Ben314]

Hé salut ben !! Ca faisait un bout de temps qu'on t'avais pas vu !! ( 2 jours)
Tu fétait pi ?? :zen:

Non, j'était au ski (j'ai pris un beau coup de soleil sur le pif...)

[benekire2]

Non, j'était au ski (j'ai pris un beau coup de soleil sur le pif...)

:ptdr: Fallait mettre de la crème !! Je dis ça mais je le fais pas ...