bonjour bonsoir a tous!
j'ai besoin d'aide pour un exercice portant sur les complexes:
"on considère les nombres complexes z(n ) définis pour tout ninférieur ou égal a 0 par la donnée de z0 où z0 est différent de 0 et de 1, et la relation de récurrence: z(n+1)= 1-(1/zn)"
1)la première question nous demande de calculer les nombres de z1 a z6 en supposant que z0= 2
ce qui nous donne: z1=1/2, z2=-1, z3=2, z4=1/2 , z5=-1, z6=2
2)ensuite il faut determiner la forme algébrique de ces meme nombres (les différents z) en partant de z0=i
on a alors: z1= 1+i, z2=1/2+1/2i, z3=-i, z4=z1, z5=z2, z6=z3
3)et c' est la 3eme question qui pose problème:
"on revient au cas général où z0 est un complexe donné. Que peut on conjecturer pour les valeurs prises par z(3n) selon les valeurs de n (entier naturel)? prouver cette conjecture.
voila, c est la que j'ai besoin de votre aide: je vois bien le lien entre les différents z (voir réponse question 2) mais je n'arrive pas conjecturer quelque chose...
merci par avance de votre aide!
Les complexes
5 messages
- Page 1 sur 1
Re: les complexes
Salut,
Il y a un petit souci dans ton calcul de z(3) quand z(0)=i.
Si z(2)=(1+i)/2 alors
z(3)= 1-2/(1+i) = (1+i-2)/(i+1) = (-1+i)/(i+1)=(-1+i)(i-1)/[i^2-1]
= [-i+1-1-i]/(-2) = -2i/(-2)=i
Conjecturer devient plus facile..!
Pour prouver ta conjecture, tu peux noter z(n)=a+ib et regarder que vaut z(n+3) (tenter une démonstration par récurrence). Par contre bien le rédiger n'est pas très simple au lycée (à voir)...(les calculs sont faciles)
Il y a un petit souci dans ton calcul de z(3) quand z(0)=i.
Si z(2)=(1+i)/2 alors
z(3)= 1-2/(1+i) = (1+i-2)/(i+1) = (-1+i)/(i+1)=(-1+i)(i-1)/[i^2-1]
= [-i+1-1-i]/(-2) = -2i/(-2)=i
Conjecturer devient plus facile..!
Pour prouver ta conjecture, tu peux noter z(n)=a+ib et regarder que vaut z(n+3) (tenter une démonstration par récurrence). Par contre bien le rédiger n'est pas très simple au lycée (à voir)...(les calculs sont faciles)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: les complexes
Salut !
Pour ta question 2, je trouve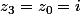 .
.
Avec les questions 1 et 2, tu peux conjecturer que pour tout ,
, 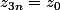 ,
, 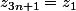 et
et 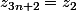 . Autrement dit, tu peux conjecturer que la suite
. Autrement dit, tu peux conjecturer que la suite ) est
est  -périodique, c'est-à-dire que pour tout
-périodique, c'est-à-dire que pour tout  ,
, 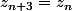 .
.
P.S. : D'ailleurs, si il y a quelqu'un qui pourrait me dire s'il y a un lien avec la géométrie projective et si la périodicité était prévisible (et comment on a construit l'exo), ça m'intéresserait beaucoup. Parce que je sais qu'il y a un lien entre composition d'homographies et matrices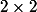 , en écrivant
, en écrivant 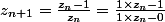 et en posant
et en posant 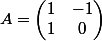 , j'obtiens
, j'obtiens 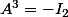 et je ne crois pas que cela soit une pure coïncidence
et je ne crois pas que cela soit une pure coïncidence 
Pour ta question 2, je trouve
Avec les questions 1 et 2, tu peux conjecturer que pour tout
P.S. : D'ailleurs, si il y a quelqu'un qui pourrait me dire s'il y a un lien avec la géométrie projective et si la périodicité était prévisible (et comment on a construit l'exo), ça m'intéresserait beaucoup. Parce que je sais qu'il y a un lien entre composition d'homographies et matrices
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: les complexes
Salut,
Ici, si tu considère) , c'est à dire (définition) l'ensemble des droites vectorielle de
, c'est à dire (définition) l'ensemble des droites vectorielle de 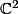 , alors le groupe
, alors le groupe ) des matrices inversibles agit naturellement sur
des matrices inversibles agit naturellement sur ) (l'image d'une droite vectorielle par une application linéaire bijective, c'est une droite vectorielle).
(l'image d'une droite vectorielle par une application linéaire bijective, c'est une droite vectorielle).
Maintenant, si tu considère une des injection naturelles de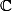 dans
dans ) , par exemple celle qui au complexe
, par exemple celle qui au complexe  associe la droite vectorielle dirigée par
associe la droite vectorielle dirigée par ) alors :
alors :
- Partant de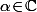 tu lui associe via l'injection la droite vectorielle de
tu lui associe via l'injection la droite vectorielle de ) dirigée par
dirigée par ) .
.
- Tu regarde l'image de cette droite vectorielle par l'application linéaire de matrice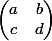 : ça te donne la droite vectorielle dirigée par
: ça te donne la droite vectorielle dirigée par ) .
.
- Modulo que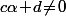 , la droite vectorielle dirigée par
, la droite vectorielle dirigée par ) , c'est la même que celle dirigée par
, c'est la même que celle dirigée par ) qui est l'image par l'injection de
qui est l'image par l'injection de 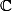 dans
dans ) du complexe
du complexe 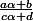 .
.
Bref, tout ça te dit que les homographies dans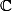 , c'est exactement la même chose que les applications linéaires bijectives de
, c'est exactement la même chose que les applications linéaires bijectives de 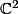 dans
dans 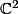 modulo deux détail :
modulo deux détail :
- L'injection dont je parle ci dessus n'est pas bijective, mais "presque" : la droite vectorielle dirigée par (1,0) n'est l'image d'aucun complexe donc si on veut que ce soit bijectif, il faut rajouter un élément à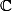 qu'on note en général
qu'on note en général  de façon à avoir une bijection de
de façon à avoir une bijection de ) sur
sur 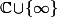 (souvent noté
(souvent noté  )
)
- Concernant les applications linéaires de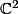 dans
dans 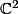 qu'on manipule, vu qu'on ne s’intéresse pas à leur action sur les vecteurs, mais sur les droites vectorielles, on n'est pas à multiplication par un scalaire prés (l'image d'une droite D par l'application linéaire L est la même que celle par l'application linéaire lambda.L) ce qui fait que le "vrai" groupe qui nous intéresse, c'est pas
qu'on manipule, vu qu'on ne s’intéresse pas à leur action sur les vecteurs, mais sur les droites vectorielles, on n'est pas à multiplication par un scalaire prés (l'image d'une droite D par l'application linéaire L est la même que celle par l'application linéaire lambda.L) ce qui fait que le "vrai" groupe qui nous intéresse, c'est pas ) mais son quotient par l'ensemble des matrice de la forme
mais son quotient par l'ensemble des matrice de la forme 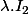 (groupe quotient appelé
(groupe quotient appelé ) avec un P comme projectif).
avec un P comme projectif).
En fait, ça signifie que les calculs matriciels, tu les fait comme d'habitude, sauf que tu n'est pas à un facteur multiplicatif prés et que par exemple,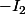 ou
ou 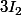 , c'est la même chose que
, c'est la même chose que 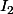 (vu que ces trois endomorphismes envoient toute droite vectorielle sur elle même).
(vu que ces trois endomorphismes envoient toute droite vectorielle sur elle même).
Oui, c'est plus que fortement lié à la géométrie projective.capitaine nuggets a écrit:P.S. : D'ailleurs, si il y a quelqu'un qui pourrait me dire s'il y a un lien avec la géométrie projective et si la périodicité était prévisible (et comment on a construit l'exo), ça m'intéresserait beaucoup. Parce que je sais qu'il y a un lien entre composition d'homographies et matrices, en écrivant
et en posant
, j'obtiens
et je ne crois pas que cela soit une pure coïncidence
Ici, si tu considère
Maintenant, si tu considère une des injection naturelles de
- Partant de
- Tu regarde l'image de cette droite vectorielle par l'application linéaire de matrice
- Modulo que
Bref, tout ça te dit que les homographies dans
- L'injection dont je parle ci dessus n'est pas bijective, mais "presque" : la droite vectorielle dirigée par (1,0) n'est l'image d'aucun complexe donc si on veut que ce soit bijectif, il faut rajouter un élément à
- Concernant les applications linéaires de
En fait, ça signifie que les calculs matriciels, tu les fait comme d'habitude, sauf que tu n'est pas à un facteur multiplicatif prés et que par exemple,
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: les complexes
Merci pour ces précisions Ben !
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 121 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
