Fonctions equa diff..
20 messages
- Page 1 sur 1
fonctions equa diff..
Salut je deplace le sujet je me suis trompé, pourriez vous m'expliquer cela :
Soit la fonction g (x) définie par :
g (x) = C_1 x^4 pour x ;) 0
g (x) = C_2 x^4 pour x ;) 0 C_1 , C_2 étant deux constantes arbitraires.
1. Montrer que la fonction g (x) est dérivable sur R.
2. En déduire la solution générale sur R de léquation différentielle : x.y 4y = 0
3. Donner une solution particulière y_0 (x) à léquation : xy 4y = -3x qui soit un polynome du 1er degré
1. Je ne vois pas ce qu'ils entendent par "dérivable sur R" deja(je ne suis pas fort en maths du tout :doh: )
salutations et remerciements.
Soit la fonction g (x) définie par :
g (x) = C_1 x^4 pour x ;) 0
g (x) = C_2 x^4 pour x ;) 0 C_1 , C_2 étant deux constantes arbitraires.
1. Montrer que la fonction g (x) est dérivable sur R.
2. En déduire la solution générale sur R de léquation différentielle : x.y 4y = 0
3. Donner une solution particulière y_0 (x) à léquation : xy 4y = -3x qui soit un polynome du 1er degré
1. Je ne vois pas ce qu'ils entendent par "dérivable sur R" deja(je ne suis pas fort en maths du tout :doh: )
salutations et remerciements.
Pour la 2... Tout d'abord je précise que y désigne une fonction de x.
Ensuite, sur ]0,+ [,
[,
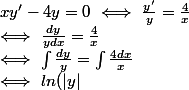=4ln(x)+C<br />\\ \Longleftrightarrow\ |y|=kx^4)
avec
donc:
 avec
avec  . De plus, la fonction nulle est une solution donc l'ensemble des solutions de l'équation homogène définies sur ]0,+
. De plus, la fonction nulle est une solution donc l'ensemble des solutions de l'équation homogène définies sur ]0,+ [ est l'ensemble des fonctions
[ est l'ensemble des fonctions  , avec K appartenant à
, avec K appartenant à  .
.
Comment fais-tu sur ]- ,0[?
,0[?
Ensuite, sur ]0,+
avec
donc:
Comment fais-tu sur ]-
Sur ]- ,0[,
,0[,
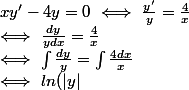=4ln(|x|)+C<br />\\ \Longleftrightarrow\ ln(|y|)=4ln(-x)+C<br />\\ \Longleftrightarrow\ |y|=k{(-x)}^4<br />\\ \Longleftrightarrow\ |y|=kx^4)
avec
On trouve les mêmes solutions que celles sur ]0,+ [. Donc en effet la puissance 4 ramène au truc positif mais... la conclusion n'est pas la bonne.
[. Donc en effet la puissance 4 ramène au truc positif mais... la conclusion n'est pas la bonne.
Remarque que toutes les solutions sont automatiquement dérivables puisqu'elles vérifient une équation différentielle, c'est-à-dire une équation faisant intervenir sa dérivée.
Pour la 3, soit P(x) un polynôme du premier degré, solution particulière de l'équation différentielle avec second membre, P(x)=ax+b.
P est solution si et seulement si xP'(x)-4P(x)=-3x

On identifie les coefficients des deux polynômes; cela nous donne a=1 et b=0. Donc P défini sur par P(x)=-3x est une solution particulière de l'équation avec second membre.
par P(x)=-3x est une solution particulière de l'équation avec second membre.
avec
On trouve les mêmes solutions que celles sur ]0,+
Remarque que toutes les solutions sont automatiquement dérivables puisqu'elles vérifient une équation différentielle, c'est-à-dire une équation faisant intervenir sa dérivée.
Pour la 3, soit P(x) un polynôme du premier degré, solution particulière de l'équation différentielle avec second membre, P(x)=ax+b.
P est solution si et seulement si xP'(x)-4P(x)=-3x
On identifie les coefficients des deux polynômes; cela nous donne a=1 et b=0. Donc P défini sur
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
