équa. diff. d'ordre 3

[egan]

Salut tout le monde,
Je cherche à trouver une fonction qui vérifie l'équa. diff.:

Je vois déjà arriver la horde de réponses prônant l'exponentielle, lol, mais j'en cherche une autre ou d'autres.
Je vais continuer de chercher encore mais j'ai du mal.
@+ Boris.

[Ericovitchi]

une piste comme ça. Si on pose on se ramène à une équation différentielle de degré moindre : z"+3z'+3z=0 qui est soluble par des moyens classiques.

[egan]

Pas bête du tout. Je cherchais justment un changement de variable judicieu.
Par contre, je ne sais pas résoudre des équa. diff. du second degrès...

[egan]

C'est bon je viens d'apprendre. ^^
Je cherche ça sur papier et je vous mets les résultats.

[Ericovitchi]

lien vers un cours qui explique comment on résout une équation différentielle comme ça.

[Black Jack]

Difficile d'aider sans tout faire.

On résout l'équation caractéristique y³ = 1
Les solutions de l'équation caractéristique sont : 1 et (-1/2 +/- ((V3)/2)i)

Solutions générales de l'équation différentielle y''' = y :

y = C.e^x + e^(-x/2) * [A.sin((V3)/2)x)) + B.cos((V3)/2)x))]

Avec A et B et C des constantes réelles.

:zen:

[Ericovitchi]

Ha oui, bien vu Black Jack, je n'y avais pas pensé mais après tout la même recette de polynôme caractéristique n'a aucune raison de ne pas s'appliquer aussi sur le degré 3.

[egan]

une piste comme ça. Si on pose on se ramène à une équation différentielle de degré moindre : z"+3z'+3z=0 qui est soluble par des moyens classiques.

En faisant le calcul, je ne vois pas comment on peut retomber sur une équation du second degré.
Comment tu as fait ?

[egan]

On résout l'équation caractéristique y³ = 1
Les solutions de l'équation caractéristique sont : 1 et (-1/2 +/- ((V3)/2)i)

Comment tu fais pour trouver les solutions complexes d'une équation comme celle là ?

[Black Jack]

Ainsi :
Poser : y = z.e^x

y' = z.e^x + z'.e^x
y'' = z.e^x + 2z'.e^x + z''.e^x
y''' = z.e^x + z'.e^x + 2.(z'.e^x + z''.e^x) + z''.e^x + z'''.e^x

y''' = y
z'.e^x + 2.(z'.e^x + z''.e^x) + z''.e^x + z'''.e^x = 0

3z' + 3z'' + z''' = 0

en posant :
z' = u --->

3u + 3u' + u'' = 0

...
*********

Mais, comme je l'ai rappelé dans mon premier message, il n'est pas nécessaire de procéder ainsi. On peut avoit les solutions de l'équation différentielle quasi immédiatement.

:zen:

[egan]

Comment tu as fait pour résoudre l'équation caractéristique y^3=1 dans C ?

[theluckyluke]

Bonjour tout le monde,

je sais que le but n'est pas forcément de donner sans justification ou méthode les solutions de l'équation différentielle (c'est mieux de les trouver évidemment) mais j'en profite pour laisser un lien vers un moteur de recherche qui est plutôt bien fait : http://www.wolframalpha.com/input/?i=y%22%27%3Dy&t=ff3tb01
et qui résout ce genre d'équations. (il fait plein d'autres choses par ailleurs)

a+

[egan]

Comment on fait pour résoudre l'équation caractéristique y^3=1 dans C ?

[theluckyluke]

Bonjour,

de manière générale, pour résoudre dans , tu cherches les solutions sous la forme . Tu cherches le réel .
Ensuite, tu trouves .

Ceci dit, cela revient dans ton cas à trouver les racines complexes troisièmes de l'unité. Les solutions sont les avec .

Pour montrer cela, tu remarques une forme générale de solutions, puisque quand tu mets au cube, il vient qui vaut 1.

Donc si tu veux résoudre dans , les solutions sont les .

a+

[Black Jack]

Comment tu as fait pour résoudre l'équation caractéristique y^3=1 dans C ?

Autre façon que celle déjà donnée :

y³-1 = 0

y = 1 est une solution évidente --> y³-1 est divisible par (y-1)

On fait la division euclidienne et on :

y³-1 = (y-1)(y²+y+1)

y²+y+1 = (y + (1/2))² - 1/4 + 1
y²+y+1 = (y + (1/2))² + 3/4
y²+y+1 = (y + (1/2))² - (i.V3/2)²
y²+y+1 = (y + (1/2) - (i.V3/2))((y + (1/2) + (i.V3/2))

Et donc:
y³-1 = (y-1)(y + (1/2) - (i.V3/2))((y + (1/2) + (i.V3/2))
...

:zen:

[egan]

Merci beaucoup à tous les deux.
C'est vrai que la factorisation, j'aurais pu y penser... Honte à moi, lol.

[egan]

D'ailleurs, qu'est-ce qu'une racine n-ième de l'unité ? J'ai rencontré ce mot plusieurs fois mais je ne sais pas ce que c'est.

[egan]

Donc si tu veux résoudre dans , les solutions sont les .
a+

Il faudrait montrer que ce sont les seules non ?

[theluckyluke]

Elles sont distinctes et tu as n racines (k=0, k=1 ..., k=n-1).

Or tu as affaire à des polynômes, et celui-ci est de degré n: .
En fait, un polynôme de degré n, ne peut pas avoir plus que n racines sinon il est nul.

Comme tu es apparemment en lycée, je vais un peu détailler.

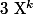
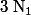
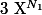
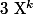
Si tu prends le polynôme (un polynôme est défini par la donnée des coefficients devant les , avec un "degré maximal", c'est-à-dire qu'il existe tel que soit le plus grand exposant du polynôme. On dit que la suite des coefficients devant les est cofinale à 0 (elle vaut 0 à partir d'un certain rang))

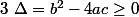
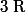
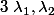
Donc si tu prends un polynôme, par exemple : avec les discriminant alors tu as deux racines dans . Donc il s'écrit encore avec les deux racines réelles. Donc il est de degré 2 (c'est le plus grand exposant) et a deux racines réelles. Il est en fait difficile d'en avoir plus sinon tu pourrais le factoriser avec un produit de et en redéveloppant, tu te rendrais compte que le polynôme serait au moins de degré 3, donc ce ne sont plus les mêmes. Le seul polynôme qui a plus de racines que son degré est le polynôme nul. Il en a d'ailleurs une infinité.
Cependant, tu n'est pas obligé d'avoir 2 racines réelles pour un polynôme de degré 2. Par exemple, si le discriminant précédent est négatif strictement, alors il n'y a pas de racines réelles, mais deux racines complexes. Tu ne pourras pas factoriser le polynôme comme précédemment dans mais tu pourras le faire dans avec des racines complexes.

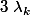
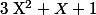
En fait, il existe un théorème (le théorème d'Alembert) qui affirme que tout polynôme dans est scindé, c'est-à-dire que tu peux l'écrire factorisé dans sous la forme avec les racines complexes. Ce qui n'est pas forcément le cas dans R, puisque certains polynôme de degré 2 (comme ne sont pas réductibles sur .

Dans le cas là, on considérais le polynôme dans . Donc on sait qu'il y a n racines dans , on les a trouvées (ce sont les racines de l'unité) donc il ne peut pas y en avoir plus, d'où l'unicité.

Voilà, j'espère avoir été assez clair. S'il y a des questions, n'hésite pas.

a+

[egan]

Merci beaucoup pour ta réponse. ^^

Ceci dit, cela revient dans ton cas à trouver les racines complexes troisièmes de l'unité. Les solutions sont les avec .

a+

Comment on sait que solutions sont forcément de cette forme ? En fait, comment détermines-tu le théta et le r ?