Fonction réciproque
22 messages
- Page 1 sur 2 - 1, 2
 fonction réciproque
fonction réciproque
bonjour j ai une fonction a une formule f(x)= 1/(x+2) +1/(x-2).
cette f est continue et décroissante sur ]-2;2[, donc elle accepte une fonction réciproque.
l ensemble de départ est IR et ensemble d arrive est ]-2;2[ mais je ne peux pas déterminer la formule de la fonction réciproque.
comment je peux la déterminer??
cette f est continue et décroissante sur ]-2;2[, donc elle accepte une fonction réciproque.
l ensemble de départ est IR et ensemble d arrive est ]-2;2[ mais je ne peux pas déterminer la formule de la fonction réciproque.
comment je peux la déterminer??
Re: fonction réciproque
Bonjour
rien de compliqué ici, parce que cela revient à savoir résoudre y=f(x) qui est ni plus ni moins que qu'une équation de second degré que tout le monde sait résoudre.
rien de compliqué ici, parce que cela revient à savoir résoudre y=f(x) qui est ni plus ni moins que qu'une équation de second degré que tout le monde sait résoudre.
Re: fonction réciproque
ahrachman a écrit:bonjour j ai une fonction a une formule f(x)= 1/(x+2) +1/(x-2).
cette f est continue et décroissante sur ]-2;2[, donc elle accepte une fonction réciproque.
l ensemble de départ est IR et ensemble d arrive est ]-2;2[ mais je ne peux pas déterminer la formule de la fonction réciproque.
comment je peux la déterminer??
Salut,
Comme a dit aviateur, tu sais que l'image y par la fonction f de x est égale à 1/(x+2)+1/(x-2) = y
Tu as donc y en fonction de x
Donc en fait si je te donne x, tu peux me calculer y.
Par contre si je te donne y (le nombre final, saurais-tu me donner un x qui convient ?)
Grâce à des justifications sur l'existence de la fonction récriproque etc, on peut avoir une réponse affirmative (oui on peut). Mais cela ne permet pas encore d'expliciter cette fonction réciproque.
Il faut donc exprimer x en fonction de y...
Donc il faut essayer d'exprimer x=..... en fonction de y...
Essaye de réduire au même dénominateur, multiplier par des quantités bien choisies les deux membres...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: fonction réciproque
merci mes potes, oui je fais tous ca et je trouve les deux solutions mais les deux solutions ne sont pas f réciproque de ma fonction
Re: fonction réciproque
Tu trouves quoi alors?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: fonction réciproque
x1=(1-racine(1-4y²))/x et x2=(1+racine(1-4y²))/x mais 1erment Df n égale pas IR 2ement lorsque je remplace y par f(1), le résultat différent 1
Re: fonction réciproque
ahrachman a écrit:x1=(1-racine(1-4y²))/x et x2=(1+racine(1-4y²))/x mais 1erment Df n égale pas IR 2ement lorsque je remplace y par f(1), le résultat différent 1
Ce ne sont pas les bonnes expressions...
Revois le calcul.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: fonction réciproque
1/(y+2) +1/(y-2) = x
(y-2+y+2)/(y²-4) = x
(y-2+y+2) = x*(y²-4)
2y = xy²-4x
xy²-2y -4x = 0
delta= 4-4*x*(-4x) = 4+16x²
tous ca me donne
y1 = (2-racine(4+16x²))/2x et y2= (2+racine(4+16x²))/2x
y1 = (1-racine(1+4x²))/x et y2 = (1+racine(1+4x²))/x
(y-2+y+2)/(y²-4) = x
(y-2+y+2) = x*(y²-4)
2y = xy²-4x
xy²-2y -4x = 0
delta= 4-4*x*(-4x) = 4+16x²
tous ca me donne
y1 = (2-racine(4+16x²))/2x et y2= (2+racine(4+16x²))/2x
y1 = (1-racine(1+4x²))/x et y2 = (1+racine(1+4x²))/x
Re: fonction réciproque
ahrachman a écrit:1/(y+2) +1/(y-2) = x
(y-2+y+2)/(y²-4) = x
(y-2+y+2) = x*(y²-4)
2y = xy²-4x
xy²-2y -4x = 0
delta= 4-4*x*(-4x) = 4+16x²
tous ca me donne
y1 = (2-racine(4+16x²))/2x et y2= (2+racine(4+16x²))/2x
y1 = (1-racine(1+4x²))/x et y2 = (1+racine(1+4x²))/x
C'est mieux mais je vois pas pourquoi tu as interverti x et y dès le début, ça risque de t'embrouiller!
Donc en fait, a priori:
x(y) = (1-racine(1+y²))/y
Ou
x(y) = (1+racine(1+y²))/y
Déjà ces formules ne sont pas définies en y=0 mais sont chacune définies pour tout y.
Est-ce que 0 n'a pas d'antécédent?
Ensuite il faut dresser le tableau de variations de f(x) et en déduire celui de f^(-1) sur ]-2;2[.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: fonction réciproque
Lostounet a écrit:ahrachman a écrit:1/(y+2) +1/(y-2) = x
(y-2+y+2)/(y²-4) = x
(y-2+y+2) = x*(y²-4)
2y = xy²-4x
xy²-2y -4x = 0
delta= 4-4*x*(-4x) = 4+16x²
tous ca me donne
y1 = (2-racine(4+16x²))/2x et y2= (2+racine(4+16x²))/2x
y1 = (1-racine(1+4x²))/x et y2 = (1+racine(1+4x²))/x
C'est mieux mais je vois pas pourquoi tu as interverti x et y dès le début, ça risque de t'embrouiller!
Donc en fait, a priori:
x(y) = (1-racine(1+4y²))/y
Ou
x(y) = (1+racine(1+4y²))/y
Déjà ces formules ne sont pas définies en y=0 mais sont chacune définies pour tout y.
Est-ce que 0 n'a pas d'antécédent?
Ensuite il faut dresser le tableau de variations de f(x) et en déduire celui de f^(-1) sur ]-2;2[.
Re: fonction réciproque
ahrachman a écrit:cette f est continue et décroissante sur ]-2;2[, donc elle accepte une fonction réciproque.
l ensemble de départ est IR et ensemble d arrive est ]-2;2[ mais je ne peux pas déterminer la formule de la fonction réciproque.
comment je peux la déterminer??
Une remarque :
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: fonction réciproque
Oui pardon j'ai oublié le 4.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: fonction réciproque
il y a deux candidats pour f^{-1}:
 et
et 
l'étude des variations de et de
et de  montre que
montre que  est la réciproque de f
est la réciproque de f
l'étude des variations de
Re: fonction réciproque
mathelot a écrit:il y a deux candidats pour f^{-1}:et
l'étude des variations deet de
montre que
est la réciproque de f
mais ces deux solution ne sont pas défini sur 0 la fonction réciproque doit etre définir sur IR ver ]-2;2[ et si je vais calculer f^{-1}(f(1)) je n trouve pas 1.
Re: fonction réciproque
ahrachman a écrit:il y'a qlq un trouver la formule de la fonction reciproque?
par continuité en y=0
Re: fonction réciproque
ahrachman a écrit:mathelot a écrit:il y a deux candidats pour f^{-1}:et
l'étude des variations deet de
montre que
est la réciproque de f
mais ces deux solution ne sont pas défini sur 0 la fonction réciproque doit etre définir sur IR ver ]-2;2[ .
Re: fonction réciproque
ahrachman a écrit:ahrachman a écrit:mathelot a écrit:il y a deux candidats pour f^{-1}:et
l'étude des variations deet de
montre que
est la réciproque de f
mais ces deux solution ne sont pas défini sur 0 la fonction réciproque doit etre définir sur IR ver ]-2;2[ .
Tu dois traiter y=0 à part...trouver x tel que f(x)=0
Et définir x(0) à part.
Ensuite suis l'indication de Mathelot: seule x2(y) convient... pour y non nul.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: fonction réciproque
Salut,
Je comprend pas trop ce que vous bricolez avec vos "formules qui se prolongent par continuité en ".
".
Quand on résous le bidule, on tombe sur du) et il me semble que plutôt que de "sortir d'un chapeau" les fameuses formules
et il me semble que plutôt que de "sortir d'un chapeau" les fameuses formules 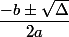 (pour ensuite tenter de corriger le tir dans le cas
(pour ensuite tenter de corriger le tir dans le cas  ...), ça me semblerait quand même infiniment plus normal de constater que (*) n'est une équation du second degré que lorsque
...), ça me semblerait quand même infiniment plus normal de constater que (*) n'est une équation du second degré que lorsque  (et que, pour
(et que, pour  , c'est une bête équation du 1er degré qu'un collégien sait parfaitement résoudre...) !!!
, c'est une bête équation du 1er degré qu'un collégien sait parfaitement résoudre...) !!!
Bref, un petit "rappel" : les "formules magiques" vu au Lycée pour résoudre , ben elle ne sont valable que pour
, ben elle ne sont valable que pour 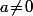 . Et lorsque
. Et lorsque 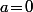 , ben là, c'est niveau (début) de collège...
, ben là, c'est niveau (début) de collège...
Je comprend pas trop ce que vous bricolez avec vos "formules qui se prolongent par continuité en
Quand on résous le bidule, on tombe sur du
Bref, un petit "rappel" : les "formules magiques" vu au Lycée pour résoudre
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: fonction réciproque
mais si je pose f^{-1}(x)= (1-racine(1+4x²))/x et f^{-1}(0)=0 après l étude la continuité de f^{-1}(x) en 0 je trouve n' est pas continuer mais lorsque je trace la Courbe de f^{-1} par symétrie d'axe x=y, elle est continue en 0. je pense ce prblm non??
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
