Détermination de la réciproque d une fonction
49 messages
- Page 3 sur 3 - 1, 2, 3
georgets555 a écrit:salut capitaine nuggets
f est une bijection de IR sur IR
f(y)=x équivaut à (y-2)^3=3(x-1) comment passer a la racine cubique il y a un problème
merci
Salut !
Je ne vois pas en quoi il y a un problème : il y a peut-être quelque chose qui t'échappe. La fonction "cube"
Autre point de vue : tu peux également essayer de voir
Tu vérifies qu'elles sont toutes bijectives, puis tu calcules leur bijection réciproque pour en déduire que
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
est ce qu il faut étudier le signe de x-1 pour passer a la racine cubique ?
salut capitaine nuggets
merci pour votre message
svp est ce qu il faut étudier le signe de x-1 pour passer a la racine cubique ?
merci
merci pour votre message
svp est ce qu il faut étudier le signe de x-1 pour passer a la racine cubique ?
merci
Je ne comprends pas pourquoi il faudrait étudier le signe de 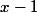 .
.
As-tu lu mon post précédent ? Je te dit très clairement avec des équivalences ce qu'on peut faire avec le cube ou la racine cubique.
D'ailleurs, si tu tiens compte de l'autre point de vue que j'ai donné, tu t'apercevra peut-être que ton égalité^3=3(x-1)) correspond à
correspond à 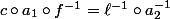 . Il ne te reste plus qu'à finir pour obtenir ce qu'on veut :
. Il ne te reste plus qu'à finir pour obtenir ce qu'on veut : 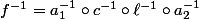
:+++:
As-tu lu mon post précédent ? Je te dit très clairement avec des équivalences ce qu'on peut faire avec le cube ou la racine cubique.
D'ailleurs, si tu tiens compte de l'autre point de vue que j'ai donné, tu t'apercevra peut-être que ton égalité
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Mais cette condition n'est pas utile.
En effet, si j'ai compris ce que tu veux faire, tu vérifier qu'on ne prend pas la racine cubique d'un nombre négatif ?
Mais la racine cubique d'un nombre négatif exite puisqu'il s'agit de la fonction réciproque d'une fonction de
Par exemple, la racine cubique de
Encore une fois, puisque la fonction racine cubique est la bijection réciproque de la fonction cube, on a quel que soit le réel
Et de manière générale, soit
1) La fonction
2) (ici,
De plus, pour tout réel
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
une fonction qui a deux expressions pour sa fonction réciproque
salut capitaine nuggets
merci pour les détails
donc deux cas a discuter x-1>0 et x-1<0 (1-x)>0
puis en applique la racine cubique
donc en obtient deux expressions de la fonctions réciproque
y=racine cub(3(x-1)+2 si x>1 et y= racine cub(3(1-x)+2 si x<1
une fonction qui a deux expressions pour sa fonction réciproque
merci
merci pour les détails
donc deux cas a discuter x-1>0 et x-1<0 (1-x)>0
puis en applique la racine cubique
donc en obtient deux expressions de la fonctions réciproque
y=racine cub(3(x-1)+2 si x>1 et y= racine cub(3(1-x)+2 si x<1
une fonction qui a deux expressions pour sa fonction réciproque
merci
49 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
