Flocon de koch
15 messages
- Page 1 sur 1
flocon de koch
Excusez-moi, je sais que ce sujet est assez récurant, mais je bloque complètement sur une question.
Le flocon de koch est une figure géométrique que lon obtient à partirdun triangle équilatéral par réitération dune transformation appliquée à chaque coté du triangle
On note Cn le nombre de segment qui constituent le flocon à létape n
Jai trouvé Cn=3*4^n-1
On note Un la longueur dun segment à létape n
Jai trouvé Un=(1/3)^n-1
Le périmètre du flocon est Pn=3*(4/3)^n-1
On note An lair du flocon à létape n
Jai calculé A1=(racinede3)/4
De létape n à létape n+1, lair est augmenté de celle de Cn triangles équilatéraux de coté Un+1
An+1 An = ((racine de 3)/12) * (4/9)^n-1
Maintenant vienne les problèmes :
Il faut calculer (An An-1) + + (A2 A1) de deux facons différentes
Jai pensé à la somme de termes consécutifs : ((racine de 3)/12) + A1 * ((1-(4/9)^n-1)/(1-(4/9))
Mais je narrive pas a trouvé la seconde solution
Et comment faire après pour calculer An ?
Merci de me donner des pistes de réflexion
Le flocon de koch est une figure géométrique que lon obtient à partirdun triangle équilatéral par réitération dune transformation appliquée à chaque coté du triangle
On note Cn le nombre de segment qui constituent le flocon à létape n
Jai trouvé Cn=3*4^n-1
On note Un la longueur dun segment à létape n
Jai trouvé Un=(1/3)^n-1
Le périmètre du flocon est Pn=3*(4/3)^n-1
On note An lair du flocon à létape n
Jai calculé A1=(racinede3)/4
De létape n à létape n+1, lair est augmenté de celle de Cn triangles équilatéraux de coté Un+1
An+1 An = ((racine de 3)/12) * (4/9)^n-1
Maintenant vienne les problèmes :
Il faut calculer (An An-1) + + (A2 A1) de deux facons différentes
Jai pensé à la somme de termes consécutifs : ((racine de 3)/12) + A1 * ((1-(4/9)^n-1)/(1-(4/9))
Mais je narrive pas a trouvé la seconde solution
Et comment faire après pour calculer An ?
Merci de me donner des pistes de réflexion
Salut,
Pour ceux qui ne connaissent pas, je met la figure :

Question 1:
On note Cn le nombre de segment qui constituent le flocon à létape n.
Ta réponse : Cn=3*4^(n-1)
Etape 0 : "à partir dun triangle équilatéral" => 3 côtés =>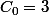
Conclusion :
=> Les expressions de Cn et Un sont bonnes si tu considères que l'étape 1 est le triangle équilatéral. Or l'étape 1, c'est après une transformation.
P.S. : Pour la suite des questions, pourrais tu nous montrer rapidement tes démonstrations.
Pour ceux qui ne connaissent pas, je met la figure :

Question 1:
On note Cn le nombre de segment qui constituent le flocon à létape n.
Ta réponse : Cn=3*4^(n-1)
Etape 0 : "à partir dun triangle équilatéral" => 3 côtés =>
Conclusion :
=> Les expressions de Cn et Un sont bonnes si tu considères que l'étape 1 est le triangle équilatéral. Or l'étape 1, c'est après une transformation.
P.S. : Pour la suite des questions, pourrais tu nous montrer rapidement tes démonstrations.
Ca dépend. Simple convention. Si l'énoncé ne précise rien d'autre, il a tout à fait le droit de dire que l'étape initiale est l'étape 1. Je trouve la phrase
Attention cependant, il ne considère que le triangle, pas les segments accolés. Attention alors aux schémas trompeurs.
peu explicite quant à la convention adoptée.Cn le nombre de segment qui constituent le flocon à létape n
Attention cependant, il ne considère que le triangle, pas les segments accolés. Attention alors aux schémas trompeurs.
confirmation
Oui je confirme que selon lexercice létape 1 est un triangle équilatéral
On a donc bien C1= 3
Et on considère que pour toutes les suites N est supérieur ou égale à 1
Il est vrai quen regardant je pense plutôt que le nombre de terme pour calculer (An An-1) + + (A2 A1) est de n.
Quant au démonstration précédente :
Cn+1 = 4 Cn
Un+1= 1/3 Un
Pn= Cn * Un
Et An+1 An = (Cn *(Un+1)^2 * racine de 3)/ 4
Doù les résultats obtenus
Mais la question suivante calculer (An An-1) + + (A2 A1) de deux facons différentes me pose vraiment problème
On a donc bien C1= 3
Et on considère que pour toutes les suites N est supérieur ou égale à 1
Il est vrai quen regardant je pense plutôt que le nombre de terme pour calculer (An An-1) + + (A2 A1) est de n.
Quant au démonstration précédente :
Cn+1 = 4 Cn
Un+1= 1/3 Un
Pn= Cn * Un
Et An+1 An = (Cn *(Un+1)^2 * racine de 3)/ 4
Doù les résultats obtenus
Mais la question suivante calculer (An An-1) + + (A2 A1) de deux facons différentes me pose vraiment problème
resuite
En utilisant la formule : ((racine de 3)/12) * ((1-(4/9)^n)/(1-(4/9)) jobtiens (3 racine de 3)/20
Et je suis désoler mais je ne vois pas en quoi cela nous arrange la seconde ecriture
Et je suis désoler mais je ne vois pas en quoi cela nous arrange la seconde ecriture
reconfirmation
je suis d'accord avec otre dernière formule. Pense vous il faut l'utiliser pour la question suivante ?
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
