Factorielles
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Bastien L.
- Membre Relatif
- Messages: 308
- Enregistré le: 12 Oct 2008, 02:33
-
 par Bastien L. » 20 Juin 2009, 16:14
par Bastien L. » 20 Juin 2009, 16:14
Bonjour à tous,
Une question toute simple:
Si je ne me trompe pas,
!}=\bigprod_{k=n-p+1}^nk)
. Comment démontrez-vous cela sans avoir recours aux "
" ou aux "On voit que
"?
Merci

-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 20 Juin 2009, 16:31
par XENSECP » 20 Juin 2009, 16:31
Par récurrence je dirais :)
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 20 Juin 2009, 16:32
par oscar » 20 Juin 2009, 16:32
Bonjour
Il sufit de remplacer n! par sa valeur = 1*2...n et ( n-p)! puis simplifier
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 20 Juin 2009, 16:32
par uztop » 20 Juin 2009, 16:32
Salut,
su tu écrits n! sous forme de produit, et (n-p)! de la même façon, quels sont les termes qui se simplifient ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 20 Juin 2009, 16:34
par XENSECP » 20 Juin 2009, 16:34
C'est des "..."

Je suis d'accord avez uztop !
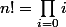
-
Bastien L.
- Membre Relatif
- Messages: 308
- Enregistré le: 12 Oct 2008, 02:33
-
 par Bastien L. » 20 Juin 2009, 16:39
par Bastien L. » 20 Juin 2009, 16:39
Ok, mais je sais que les matheux n'aiment pas les (
), avec raison
Alors, en écrivant:
!}=\frac{\bigprod_{k=1}^{n}k}{\bigprod_{k=1}^{p}k}=\bigprod_{k=n-p+1}^{n})
?
-
Bastien L.
- Membre Relatif
- Messages: 308
- Enregistré le: 12 Oct 2008, 02:33
-
 par Bastien L. » 20 Juin 2009, 16:40
par Bastien L. » 20 Juin 2009, 16:40
Si je puis me permettre, XENSECP, il vaudrait mieux que ton produit débute à 1
;-)
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 20 Juin 2009, 17:06
par uztop » 20 Juin 2009, 17:06
Bastien L. a écrit:Ok, mais je sais que les matheux n'aiment pas les (
), avec raison
Alors, en écrivant:
!}=\frac{\bigprod_{k=1}^{n}k}{\bigprod_{k=1}^{p}k}=\bigprod_{k=n-p+1}^{n})
?
il y a une faute (de frappe je pense) dans ton post:
!}=\frac{\bigprod_{k=1}^{n}k}{\bigprod_{k=1}^{n-p}k})
Tous les termes allant de 1 à n-p sont présents au numérateur et au dénominateur, donc ils se simplifient.
Il reste donc les termes suivants, c'est à dire pour k allant de (n-p+1) à n
-
Bastien L.
- Membre Relatif
- Messages: 308
- Enregistré le: 12 Oct 2008, 02:33
-
 par Bastien L. » 20 Juin 2009, 17:08
par Bastien L. » 20 Juin 2009, 17:08
Ok, après avoir explicité le numérateur et le dénominateur, la suite est évidente
Merci d'avoir relevé la faute de frappe
:-)
-
abdelmoaiz
- Messages: 5
- Enregistré le: 20 Juin 2009, 22:44
-
 par abdelmoaiz » 21 Juin 2009, 02:02
par abdelmoaiz » 21 Juin 2009, 02:02
\sum_{n=1}^{+\infty}\frac{1}{n^2}=\frac{\pi^2}{6}
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 21 Juin 2009, 10:00
par XENSECP » 21 Juin 2009, 10:00
Bastien L. a écrit:Si je puis me permettre, XENSECP, il vaudrait mieux que ton produit débute à 1

Ouais ouais j'ai tapé vite ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
?