Etude de fonctions du type f o g
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
aCe77
- Membre Naturel
- Messages: 11
- Enregistré le: 01 Déc 2006, 21:10
-
 par aCe77 » 13 Jan 2007, 15:31
par aCe77 » 13 Jan 2007, 15:31
Bonjour, j'ai un petit problème avec un exercice.
Il s'agit de donner l'
ensemble de définition de la fonction g et dresser son
tableau de variation.
Sachant que pour la
fonction f définie sur [-2 , 2] , on a le tableau de variation ci-dessous.
 g(x) = f(x²)
g(x) = f(x²)Je ne sais pas comment faire mais j'ai quand meme commencer par faire: g(x)=(f o u)(x) où u: x-->x²
g(x)=f(u(x))
Comment trouver le domaine de définition et les variations de g avec ceci?
Merci de votre aide.
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 13 Jan 2007, 15:38
par Zebulon » 13 Jan 2007, 15:38
Bonjour,
aCe77 a écrit:g(x) = f(x²)Je ne sais pas comment faire mais j'ai quand meme commencer par faire: g(x)=(f o u)(x) où u: x-->x²
g(x)=f(u(x))
c'est bien d'avoir introduit u.
Comment trouver le domaine de définition ?
J'appelle

le domaine de définition de f et
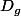
le domaine de définition de g.
On a :
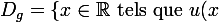\in D_f\})
et les variations de g avec ceci?
Je te renvoie à ton cours sur les variations des fonctions composées.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités

