Equation différentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 10 Jan 2007, 19:50
par Melkor » 10 Jan 2007, 19:50
Salut, j'ai un exo sur les équations différentielles et j'y comprends rien du tout
:cry:
Resoudre l'équation y'+2xy = 2x avec comme condition : y(0) = 2
Si qqun peut maider en expliquant bien ce serait cool merci d'avance
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 10 Jan 2007, 19:55
par fahr451 » 10 Jan 2007, 19:55
multiplie les deux membres par exp (x^2) et reconnais les dérivées de ...
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 10 Jan 2007, 19:57
par Melkor » 10 Jan 2007, 19:57
euh d'accord mais pourquoi?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 10 Jan 2007, 19:58
par fahr451 » 10 Jan 2007, 19:58
justement pour reconnaitre certaines dérivées...
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 10 Jan 2007, 20:00
par Melkor » 10 Jan 2007, 20:00
j'ai fait comme tu m'as dit je me trouve donc avec
y'e^x² + 2xye^x² = 2xe^x²
et je sais que 2xe^x² est la dérivé de e^x²
amis après je vois pas trop pourquoi j'ia fait ça :hein:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 10 Jan 2007, 20:08
par fahr451 » 10 Jan 2007, 20:08
le premier membre est également la dérivée d une fonction "simple"
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 10 Jan 2007, 20:17
par Melkor » 10 Jan 2007, 20:17
le premier membre? donc y'e^x² a pour primitive y/3(e^x^3)
mais l'idée c'est de transformer l'équation sous la forme y' = ky ou y' = ay +b ?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 10 Jan 2007, 20:21
par fahr451 » 10 Jan 2007, 20:21
NON le premier membre comporte deux termes
et est la dérivée de yexpx^2
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 10 Jan 2007, 20:48
par Melkor » 10 Jan 2007, 20:48
ah ok
y'e^x² + y2xe^x² à pour primitive ye^x²
j'ai donc à gauche ma dérivé et à droite ma fonction de base?
alors mon équation donne
y'e^x² + y2xe^x² = Cye^x² avec C comme réel constante
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 11 Jan 2007, 03:09
par fahr451 » 11 Jan 2007, 03:09
l 'équation est équivalente (car l exp ne s 'annule pas) à
F' = G' c'est à dire à F = G +cst d' où y
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 11 Jan 2007, 07:48
par allomomo » 11 Jan 2007, 07:48
Salut,
L'équation différententielle :
 : y'+2xy=2x)
La solution de l'équation homogène
=Ce^{-\int_{0}^{t}2xdx}, C\in\mathbb{R})
Il y a une solution particulière évidante
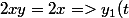=1)
La solution générale est donnée par l'expression :
=y_0(t)+y(_1t)=Ce^{-t^2}+1)
Or on a une condition particulière
=C+1=2 =>C=1)
Donc LA solution est :
=e^{-t^2}+1})
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 11 Jan 2007, 18:39
par Melkor » 11 Jan 2007, 18:39
merci, je me suis apercu également que mon équation diff n'était pas au programme, ça explique pourquoi j'y arrivais pas lol
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 11 Jan 2007, 19:55
par allomomo » 11 Jan 2007, 19:55
mais si, elle est au programme
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 11 Jan 2007, 21:00
par Melkor » 11 Jan 2007, 21:00
Bah pas au programme de Terminale S en tout cas lol
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
