Ensemble de définition

par **CBMaths_prof** » 11 Aoû 2015, 20:43

Elsapseudo a écrit:D'accord et bien merci à tous pour votre sympathique aide!!
Et aussi, une autre petite question..^^ Que dois-je faire lorsqu'il est dit d'étudier la derivabilité de f en 0 ?

Il faut remarquer que la fonction :

s'écrit

Si on note

et

, est-ce que les deux fonctions g et h sont dérivables en 0 ?

par **Elsapseudo** » 11 Aoû 2015, 20:49

CBMaths_prof a écrit:Il faut remarquer que la fonction :

s'écrit

Si on note et , est-ce que les deux fonctions g et h sont dérivables en 0 ?

Comment je fais pour savoir? C'est avec la limite?

par **CBMaths_prof** » 11 Aoû 2015, 20:54

As-tu déjà vu les caractéristiques de la fonction

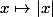
? Domaine de définition ? Dérivabilité ? Variations de la fonction ?

par **Elsapseudo** » 11 Aoû 2015, 20:56

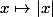
CBMaths_prof a écrit:As-tu déjà vu les caractéristiques de la fonction ? Domaine de définition ? Dérivabilité ? Variations de la fonction ?

Oui car je suis en première S mais pour vous dire je ne me souviens pas trop avoir travaillé là-dessus puisque la seule chose qu'on faisait était de dériver des fonctions puis etudier leur variation.

par **CBMaths_prof** » 11 Aoû 2015, 20:57

Donc tu as vu que la fonction

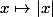
n'est pas dérivable en 0 ?

par **Elsapseudo** » 11 Aoû 2015, 20:58

Elsapseudo a écrit:Oui car je suis en première S mais pour vous dire je ne me souviens pas trop avoir travaillé là-dessus puisque la seule chose qu'on faisait était de dériver des fonctions puis etudier leur variation.

Et il me semble ne jamais avoir vu les caractéristique de x->|x|

par **Elsapseudo** » 11 Aoû 2015, 21:00

Non je ne crois pas...

par **capitaine nuggets** » 11 Aoû 2015, 21:03

Sinon, tu peux utiliser la définition de la dérivabilité en un point.
Puisque le point en question est situé sur une valeur d'abscisse interdite, f est dérivable en 0 si et seulement si f est dérivable à gauche et à droite en 0 et si

par **CBMaths_prof** » 11 Aoû 2015, 21:03

Bon, sinon est-ce qu'on te demande de calculer

?

par **Elsapseudo** » 11 Aoû 2015, 21:12

Omg j'ai jamais vu ça c'est la cata... Je vais essayer la technique de capitaine nuggets... Et non il ne demande pas de calculer f'(x) mais ducoup je dois le faire?

par **CBMaths_prof** » 11 Aoû 2015, 21:15

Elsapseudo a écrit:Omg j'ai jamais vu ça c'est la cata... Je vais essayer la technique de capitaine nuggets... Et non il ne demande pas de calculer f'(x) mais ducoup je dois le faire?

Si tu veux utiliser la méthode de Capitaine Nuggets, oui, il faudra passer par le calcul de la dérivée.

Mais le mieux serait de nous donner l'énoncé entier de ton exercice pour qu'on puisse savoir ce qu'il en retourne au final.

par **capitaine nuggets** » 11 Aoû 2015, 21:20

Après la méthode de CBMAths_prof n'est pas compliquée non plus : on décompose la fonction

en produit g\imes h de deux fonctions (dont une pas dérivable en 0). Si une des deux fonctions g ou h n'est pas dérivable en 0 alors leur produit ne le sera pas plus.

(après tu peux considérer ça comme un petit truc à savoir : la fonction

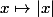
est dérivable partout sauf en

).

par **Elsapseudo** » 11 Aoû 2015, 21:23

CBMaths_prof a écrit:Si tu veux utiliser la méthode de Capitaine Nuggets, oui, il faudra passer par le calcul de la dérivée.

Mais le mieux serait de nous donner l'énoncé entier de ton exercice pour qu'on puisse savoir ce qu'il en retourne au final.

Et bien l'énoncé c'est exactement ce que je vous ai dit, il était demandé au début de determiner l'ensemble de def que je vous ai donné tout a l'heure et la question 2 est "etudier la derivabilité de f en 0" sauf que j'ai jamais fait ca!! J'ai juste appris cette année a dériver une fonction...!

par **Elsapseudo** » 11 Aoû 2015, 21:31

Attendez attendez j'ai aussi vu comment on calcule le taux d'accroissement et on pouvait donc répondre à ce genre de question "en déduire que f est derivable en 1...." C'est peut etre ca non? C'est avec cette formule je crois :

f(a+h)-f(a) / h

par **CBMaths_prof** » 12 Aoû 2015, 08:27

Cela donne quoi avec le taux d'accroissement ?

par **Elsapseudo** » 12 Aoû 2015, 13:40

CBMaths_prof a écrit:Cela donne quoi avec le taux d'accroissement ?

Et bien je crois que ça fait h, mais je ne suis pas sûre.

par **capitaine nuggets** » 12 Aoû 2015, 14:11

Pose le calcul, tu dissiperas tout doute :++:

Calcule

pour

et regarde si

.

par **Carpate** » 12 Aoû 2015, 14:40

capitaine nuggets a écrit:Pose le calcul, tu dissiperas tout doute :++:

Calcule pour et regarde si .

Le problème est que f n'est pas définie en 0

En multipliant haut et bas f par la quantité conjuguée du dénominateur, on obtient

Quand

,

Quand

,

On peut donc prolonger f en 0 par continuité et fixer f(0)=0
Ce qui permet de calculer les limites de

selon que h tend vers 0 par valeurs inférieures et supérieures.
Tu trouveras que ces limites sont de signes opposés et donc que f n'est pas dérivable en 0

par **Elsapseudo** » 12 Aoû 2015, 18:03

Carpate a écrit:Le problème est que f n'est pas définie en 0

En multipliant haut et bas f par la quantité conjuguée du dénominateur, on obtient
Quand ,
Quand ,
On peut donc prolonger f en 0 par continuité et fixer f(0)=0
Ce qui permet de calculer les limites de selon que h tend vers 0 par valeurs inférieures et supérieures.
Tu trouveras que ces limites sont de signes opposés et donc que f n'est pas dérivable en 0

Si je calcule le taux d'accroissement selon la technique de carpate je trouve 1. Mais normalement je devrai trouver 0 non?

par **Landstockman** » 12 Aoû 2015, 18:10

Il doit y avoir deux taux d'accroissements différents en 0 (taux en 0- et en 0+ différents), ce qui explique que la fonction n'est pas continue en 0

Ensemble de définition

Qui est en ligne