Ensemble de définition

[Elsapseudo]

Bonsoir à tous,

J'ai un petit problème, je n'arrive pas à savoir l'ensemble de définition de la fonction suivante :

x|x| / x+1 -1 (Ici le -1 n'est pas sous la racine)

Merci d'avance pour votre aide...

Cordialement

[CBMaths_prof]

Bonsoir,

La fonction est bien :

???

[Elsapseudo]

Oui la fonction est bien la suivante!

[capitaine nuggets]

Applique ce que tu as vu en seconde :
1) le dénominateur ne dois jamais s'annuler ;
2) ce qu'il y a sous une racine carré doit toujours être positif.

:+++:

[CBMaths_prof]

Donc pour que la fonction soit bien définie, il faut que le dénominateur ne soit pas nul... Quelle est le dénominateur ? Comment trouver les pour que le dénominateur de la fonction soit nul ?

[Elsapseudo]

Est-ce que ca serait donc [-1+infini[ ?

[CBMaths_prof]

Sauf que dans ton intervalle proposé, il y a une valeur qui est une valeur interdite pour ta fonction. Laquelle ?

[capitaine nuggets]

Peut-être bien ; si tu as bien mené tes calculs, la réponse devrait être correcte.
Si tu tentes une réponse sans vraiment t'être penché sur la question, tu as toutes les chances de t'être planté.
Déjà, est une valeur interdite donc il ne peut pas être dans le domaine.
Revois tes calculs :+++:

[Elsapseudo]

Attendez attendez, pourquoi -1 est une valeur interdite?

[CBMaths_prof]

Peut-être bien ; si tu as bien mené tes calculs, la réponse devrait être correcte.
Si tu tentes une réponse sans vraiment t'être penché sur la question, tu as toutes les chances de t'être planté.
Déjà, est une valeur interdite donc il ne peut pas être dans le domaine.
Revois tes calculs :+++:

Il me semble qu'une racine carrée peut être nulle, non ?

[Elsapseudo]

Il me semble qu'une racine carrée peut être nulle, non ?

Je suis d'accord! Enfin je crois....

[CBMaths_prof]

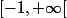
As-tu vérifié qu'il n'y a pas une valeur dans qui annule le dénominateur de la fonction ?

[capitaine nuggets]

Aille ! Oui je me suis emmêlé les pinceaux : 0 est un valeur interdite car elle annule le dénominateur !
(j'avais oublié le "-1" du dénominateur...)

[Elsapseudo]

Oui oui j'ai vérifié et il y a 0 c'est sur mais est-ce que si je marque "pour x différent de 0, Df = [-1;+infini[ ca marche?" Ou je dois marquer l'intervalle avec l'union?

[Landstockman]

C'est 0! Mais alors je fais [-1;0[ U ]0;+infini[ ?
Ou est ce que ca marche si je dis pour x différent de 0, Df = [-1;+infini[ ?

C'est ça !
Tu peux dire Df = [-1;0[ U ]0;+infini[ ou Df = [-1+infini[ - {0}

Déjà, -1 est une valeur interdite donc il ne peut pas être dans le domaine.

-1 n'est pas valeur interdite puisque l'image de -1 est 1

:lol3:

[CBMaths_prof]

Oui oui j'ai vérifié et il y a 0 c'est sur mais est-ce que si je marque "pour x différent de 0, Df = [-1;+infini[ ca marche?" Ou je dois marquer l'intervalle avec l'union?

Oui, tu dois utiliser une union de deux intervalles en excluant le réel 0.

[Elsapseudo]

Aille ! Oui je me suis emmêlé les pinceaux : 0 est un valeur interdite car elle annule le dénominateur !
(j'avais oublié le "-1" du dénominateur...)

Vous êtes excusé! En effet je ne comprenais pas pq -1 aurait été une valeur interdite

[Elsapseudo]

Oui, tu dois utiliser une union de deux intervalles en excluant le réel 0.

D'accord et ca ne marche pas si je mets ma phrase du début qui dit que x est différent de 0?

[capitaine nuggets]

Tu peux l'écrire de deux manières ou .

:++:

[Elsapseudo]

D'accord et bien merci à tous pour votre sympathique aide!!
Et aussi, une autre petite question..^^ Que dois-je faire lorsqu'il est dit d'étudier la derivabilité de f en 0 ?