Diviseurs et limite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Aoû 2010, 15:09
par Nightmare » 20 Aoû 2010, 15:09
Hello,
Je note

le nombre d'entiers i inférieurs à n tels que le reste de la division de n par i soit supérieur à

.
Calculer

:happy3:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Aoû 2010, 16:24
par benekire2 » 20 Aoû 2010, 16:24
Je m'y met , on va déjà conjecturé le résultat ... :zen:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Aoû 2010, 16:53
par benekire2 » 20 Aoû 2010, 16:53
Est-ce que on compte ceux qui sont égaux à i/2 ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Aoû 2010, 17:13
par Nightmare » 20 Aoû 2010, 17:13
Oui :happy3:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Aoû 2010, 17:26
par benekire2 » 20 Aoû 2010, 17:26
J'ai essayé pour 10 et 50 et je trouve approximativement 1/3 , je conjecture donc que cette suite converge vers 1/3 , est-ce bon ?
Sinon j'ai cherché un peu la preuve, mais bon je ne vois rien à l'horizon, il faut que je montre que

est bornée.
Une petite indic ? :we:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Aoû 2010, 18:18
par Nightmare » 20 Aoû 2010, 18:18
Salut,
Non, ça ne converge pas vers 1/3. Je te laisse chercher, ce n'est pas facile, je reviendrai ce soir apporter un indice si besoin.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Aoû 2010, 18:24
par benekire2 » 20 Aoû 2010, 18:24
ok ok , t'en fais pas, a moins que je devienne une lumière, j'y serrai toujours ce soir :zen:
Cela dit, pour tuer le temps je vais prendre le cas n=100 ... je vais essayer de regarder "où se déposent les valeurs"
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Aoû 2010, 19:06
par benekire2 » 20 Aoû 2010, 19:06
Tient c'est bizarre, je trouve qu'il y en a 31 qui marchent pour n=100 soit d_100/100=0.31 ....
Je veut bien l'indice :zen:
Salut!
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Aoû 2010, 21:10
par Nightmare » 20 Aoû 2010, 21:10
Une approximation du résultat attendu serait 0.3862...
Premier indice : Il faudrait pouvoir avoir une formule pour d(n). Pour cela, je te propose de partir simplement de la définition de la division Euclidienne :
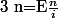i+reste.)
Avec ceci, essaye de trouver une condition pour qu'un entier i vérifie l'hypothèse. Une fois ceci fait, la suite fera appel à l'intégration (cette partie sera difficilement rigoureusement justifiable niveau lycée, néanmoins, sans trop se préoccuper de la rigueur, on arrive facilement au résultat).
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Aoû 2010, 21:13
par benekire2 » 20 Aoû 2010, 21:13
ok ok, je vais chercher une écriture de d_n ...
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Aoû 2010, 21:38
par benekire2 » 20 Aoû 2010, 21:38
Euh :hein: Je cherche, mais j'ai pas bien beaucoup de "pistes" je ne vois pas comment je vais pouvoir caractériser notre reste,
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Aoû 2010, 21:48
par Nightmare » 20 Aoû 2010, 21:48
Par exemple, dire que le reste de la division de i par n est supérieur à i/2 peut s'écrire
i < i)
, soit
\] < 2)
Avec ça, tu devrais pouvoir trouver une formule pour d(n).
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Aoû 2010, 21:55
par benekire2 » 20 Aoû 2010, 21:55
Ok, je vais y réfléchir demain matin, là je suis fatigué :zen:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 21 Aoû 2010, 10:07
par benekire2 » 21 Aoû 2010, 10:07
Bonjour,
Déjà, il ne peut pas y avoir de formule en fonction de n, mais même une formule en fonction de la décomposition en produit de facteurs premiers je ne trouve vraiment rien, je suis -encore- bloqué. Comme dois-je faire ?
Merci,
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Aoû 2010, 10:25
par Nightmare » 21 Aoû 2010, 10:25
Eh bien, c'était presque terminé. Comme on a toujours
\])
, on en déduit que :
\])
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 21 Aoû 2010, 10:30
par benekire2 » 21 Aoû 2010, 10:30
Ah oui, c'est a dire que moi je m'attendait à un truc un peu miracle ...
Pour la suite je n'ai pas fait d'intégration encore (enfin juste niveau Term) mais ça ressemble soit à des sommes de riemann soit à des sommes de darboux ( je sais pas, je vais voir), enfin bref, je vais faire un dessin,
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 21 Aoû 2010, 14:26
par benekire2 » 21 Aoû 2010, 14:26
Re,
Décidément, j'arrive vraiment a rien sur cet exo :briques:
Cette somme ressemble a rien de ce que je connait, et t'as dit que ça se résolvait "assez facilement" par intégration.
Pourrait-tu me donner (encore...) une autre indication stp ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Aoû 2010, 15:05
par Nightmare » 21 Aoû 2010, 15:05
Tu l'as dit, c'est une somme de Riemann, sauf que la fonction a une singularité en une borne, c'est là où ça se complique un peu.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 21 Aoû 2010, 15:14
par Doraki » 21 Aoû 2010, 15:14
Il manque pas une partie entière dans la somme ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Aoû 2010, 15:33
par Nightmare » 21 Aoû 2010, 15:33
Doraki a écrit:Il manque pas une partie entière dans la somme ?
Si, bien entendu, c'est
\))
:happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités