Trouver le nombre de diviseurs

[audinette]

Bonjour.

Quels sont les nombres inférieurs à 10 qui possèdent exactement trois diviseurs?

J'ai la réponse mais pas la méthode...

merci

[beagle]

si on compte diviseurs le 1, et le nombre lui-mème,
alors déjà de 3 on passe à 1 seul diviseur.
Donc ne marchent que les carrés, sinon les rectangles auront déjà 4 diviseurs.

donc carrés de 2, de 3
et ensuite cela déborde de 10

c'est ça?

[audinette]

non pas vraiment...

[Sylviel]

je suppose qu'ils comptent effectivement le nombre et 1. La meilleure méthode a mon avis est d'être systématique :
diviseur de 1 : 1 => 1 diviseur
diviseur de 2 : 1 et 2 => 2 diviseurs
diviseur de 3 : 1 et 3 => 2 diviseurs
diviseur de 4 : 1 et 2 => 2 diviseurs
diviseur de 5 : 1 et 5 => 2 diviseurs
diviseur de 6 : 1 et 2 et 3 => 3 diviseurs
diviseur de 7 : 1 et 7 => 2 diviseurs
diviseur de 8 : 1 et 2 et 4 => 3 diviseurs
diviseur de 9 : 1 et 3 => 2 diviseurs

donc 6 et 8.

[audinette]

la réponse est 4 et 9 il y a toute une formule mais je ne sais pas laquelle c'est !!

[beagle]

j'avais dit carré de 2 et 3,
tu me réponds non, c'est 4 et 9,
hum, hum

Il n' y a pas de formule pour ce truc, si 1 et nombre sont déjà deux diviseurs, la seule façon d'avoir seulement 3 diviseurs c'est de n'en avoir qu'un seul supplémentaire,
or un diviseur tout seul, à part les carrés de ce seul diviseur, je ne vois pas comment cela serait possible.
Si le troisième diviseur avait un quotient différent, alors quotient différent ferait quatrième diviseur.

je ne vois pas quelle belle formule aurait un intérèt dans ce truc.

on peut dire plus proprement ce que je raconte avec n = kxk'
mais bon

les solutions sont des couples si k est diviseur alors k' l'est aussi,
pour avoir un nombre impair de diviseurs il faut qu'un couple de kk' soit tel que kk' et k'k compte pour 1, donc k=k'

[audinette]

Oui j'avais lu trop vite...les maths et moi ça fait deux...au carré!! :doh:

[beagle]

Sinon,de quelle formule parlais-tu?
Cela ressemblait à quoi?

[oscar]

Soit N = a ^ * b ^n
Le nombre de diviseurs d' un nombre est donné par la formule k = ( m+1)(n+1)

Exemple N = 2 ² * 3^3

k =( 2+1) ( 3+1)= 12

[audinette]

c'était en fait une formule pour trouver le nombre de diviseurs...

D'après le théorème suivant:
soit n un entier naturel, alors on peut écrire n=p1^µ1 x p2 ^µ2 x...pk^µk
où les entiers naturels p1,p2..., pk sont premiers et distincts, et où µ1, µ2 sont des nombres naturels...

[audinette]

merci oscar, c'est cette formule mais ce n'est pas le résultat attendu...

[beagle]

merci Oscar,
donc ça fait classe effectivement
(m+1)(n+1)= 3
il faut m=0 et n=2, donc faut un carré
avec m=1 pas de soluces

et si (m+1)(n+1)(p+1)=3
c'est pas très facile non plus sans revenir au cas précédent en mettant des 0

[Ben314]

Si où 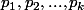sont des nombres premiers distincts et des entiers, alors tout les diviseurs positifs de n sont de la forme 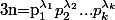avec [donc choix possible] [donc choix possible] ... (donc choix possible).
Au total, il y a donc diviseurs possible [y compris 1 qui correspond à prendre les nuls et n lui même qui correspond à prendre les égaux aux ]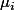

Cette formule donne le cas général, mais n'est vraiment pas indispensable dans le cas où l'on cherche seulement les nombres ayant exactement trois diviseurs : le raisonnement de Beagle est largement suffisant dans ce cas.