Diviseurs et limite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 31 Aoû 2010, 09:56
par Doraki » 31 Aoû 2010, 09:56
J'crois que c'est plutôt la somme des 1/(2k²+3k+1).
Mais c'est mieux de laisser sous la forme 2*(1/3 - 1/4 + 1/5 - 1/6 ...)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 31 Aoû 2010, 10:01
par benekire2 » 31 Aoû 2010, 10:01
Ouais c'est 2k² et non k² excuse !
Ca y est enfin fini :zen:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 31 Aoû 2010, 13:09
par Nightmare » 31 Aoû 2010, 13:09
Salut,
tout ça se calcule :
\)\)dt=\Bigsum_{n=1}^{+\infty} \Bigint_{\frac{1}{n+1}}^{\frac{1}{n}} E\(2\(\frac{1}{t}-E\(\frac{1}{t}\)\)\)dt)
Assez rapidement, on a que
\)\)dt=\frac{1}{n+\frac{1}{2}}-\frac{1}{n+1})
puis :
+1+\frac{1}{N+1})
.
Or la suite
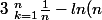\)_{n})
converge, et
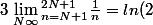)
On obtient alors rapidement
\)\)dt=ln(4)-1\simeq 0.386..)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 31 Aoû 2010, 13:33
par benekire2 » 31 Aoû 2010, 13:33
D'accord ! C'est bien mieux que ce que j'avais fait !!!
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 31 Aoû 2010, 19:36
par benekire2 » 31 Aoû 2010, 19:36
Bon, j'ai relu atentivement ton post,
Un truc m'interpelle :
\)\)dt=\frac{1}{n+\frac{1}{2}}-\frac{1}{n+1})
Comment fait-tu pour le montrer ? La fonction n'est pourtant pas continue sur cet intervalle , Pour n=1 si on prend t=3/4 alors f(t)=0
Sinon, il y a un deuxième truc qui m'embête c'est ça :
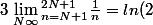)
Comment fait on pour le montrer ?
Merci :happy3:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 31 Aoû 2010, 19:40
par Doraki » 31 Aoû 2010, 19:40
Il la découpe en deux.
Un bout de 1/(n+1) à 1/(n+1/2), et un bout de 1/(n+1/2) à 1/n.
Et la fonction est constante sur l'intérieur de chacun de ces intervalles.
(me demande pas d'expliquer la ligne d'après)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 31 Aoû 2010, 19:44
par benekire2 » 31 Aoû 2010, 19:44
Non c'est bon pour la ligne d' après, enfin c'est un développement il me semble, enfin ça passe. C'est
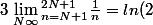)
qui me pose problème , tu peut m'expliquer rapido stp ?
Merci, et désolé ..
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 31 Aoû 2010, 19:48
par Doraki » 31 Aoû 2010, 19:48
Là il faut voir que ça correspond à une somme de riemann pour l'intégrale de 1 à 2 de 1/t dt.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 31 Aoû 2010, 19:50
par benekire2 » 31 Aoû 2010, 19:50
Doraki a écrit:Là il faut voir que ça correspond à une somme de riemann pour l'intégrale de 1 à 2 de 1/t dt.
Ok, je verrais tout ça demain, merci beaucoup Doraki !
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Sep 2010, 15:34
par benekire2 » 03 Sep 2010, 15:34
Bon et bien j'ai encore un problème

J'ai écrit
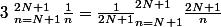
Donc ici clairement notre fonction est x--> 1/x et on aimerait bien l'intégrer entre 1 et 2. Seulement voilà, j'y arrive pas ( pas pour intégrer, pour pouvoir dire que c'est une somme de riemann)
Quelqu'un pourrait me passer un coup de main ?
Merci à vous :happy3:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Sep 2010, 22:11
par benekire2 » 03 Sep 2010, 22:11
Bon et bien j'ai encore un problème

J'ai écrit
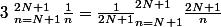
Donc ici clairement notre fonction est x--> 1/x et on aimerait bien l'intégrer entre 1 et 2. Seulement voilà, j'y arrive pas ( pas pour intégrer, pour pouvoir dire que c'est une somme de riemann)
Quelqu'un pourrait me passer un coup de main ?
Merci à vous :happy3:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 04 Sep 2010, 11:46
par benekire2 » 04 Sep 2010, 11:46
Salut,
Finalement j'ai trouvé et c'était pas très dur, j'ai changé d'indice et je me suis ramené à une somme de riemann de 0 à 1 de 1/(1+x) qui me donne ln(2) .
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 04 Sep 2010, 13:20
par benekire2 » 04 Sep 2010, 13:20
Puisque je suis sur cette somme de Riemann, je me demande, comment est-ce que je peut faire pour en avoir un développement asymptotique ? Je sais que c'est possible à faire mais je ne vois pas comment . Je continue de chercher de mon côté mais si quelqu'un peut me dire comment faire je serais ravi !
Merci bien !
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 04 Sep 2010, 18:00
par benekire2 » 04 Sep 2010, 18:00
Puisque je suis sur cette somme de Riemann, je me demande, comment est-ce que je peut faire pour en avoir un développement asymptotique ? Je sais que c'est possible à faire mais je ne vois pas comment . Je continue de chercher de mon côté mais si quelqu'un peut me dire comment faire je serais ravi !
Merci bien !
PS. Il s'agit de donner un Développement asymptotique de
+k})
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Sep 2010, 18:03
par Nightmare » 04 Sep 2010, 18:03
Salut,
tu peux commencer par chercher une relation de récurrence par exemple !
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 04 Sep 2010, 18:04
par benekire2 » 04 Sep 2010, 18:04
Nightmare a écrit:Salut,
tu peux commencer par chercher une relation de récurrence par exemple !
Salut,
Qu'est-ce que tu entend par relation de récurrence ici ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Sep 2010, 18:06
par Nightmare » 04 Sep 2010, 18:06
du type u(n+1)=f(u(n))
:)
-
AL-kashi23
- Membre Rationnel
- Messages: 765
- Enregistré le: 14 Aoû 2007, 10:59
-
 par AL-kashi23 » 04 Sep 2010, 18:08
par AL-kashi23 » 04 Sep 2010, 18:08
Salut,
ça veut dire simplement "Tu poses
+k})
et tu cherches une relation de récurrence entre les termes de ta suite, un+1, un, " je pense.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 04 Sep 2010, 18:14
par benekire2 » 04 Sep 2010, 18:14
D'accord, après calculs j'obtiens

Et après je dois procéder comment ? En fait je sais que Un et Un+1 on même développement asymptotique, mais j'arrive as a l'utiliser ..
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 04 Sep 2010, 19:45
par benekire2 » 04 Sep 2010, 19:45
D'accord, après calculs j'obtiens

Comment puis-je continuer ?
Merci beaucoup !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités

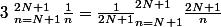

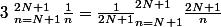
+k})
