Dérivation

par **razel** » 07 Juil 2015, 00:15

Salut,je rencontre quelques difficulté avec ce problème.

Soit f une fonction et soit a un réel qui appartient à un ensemble ouvert I tel que I est inclus dans le domaine de définition de f.

1) Mq si f est dérivable en a;

= f(a)
2) Est-ce que la proposition inverse (B implique A si j'ai mal traduit l'exo) est vraie?

J'ai pensé à montrer que

- f(a) = 0

f est dérivable en a

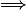
= f(a)

- f(a) = f(a) - f(a) = 0

C'est trop beau pour être vrai, et en plus je doute de la première implication.

Un coup de main serait le bienvenu :help: :lol3:

par **mathelot** » 07 Juil 2015, 07:57

si f est dérivable en x=a

on pose

avec

d'où

donc

par **razel** » 07 Juil 2015, 11:21

Merci pour ton aide, mais j'aimerais savoir s'il y a une erreur dans ce que j'ai écrit.

par **mathelot** » 07 Juil 2015, 11:29

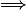
razel a écrit:f est dérivable en a = f(a)

pourquoi cette implication est-elle vraie ?

par **razel** » 07 Juil 2015, 11:37

Euh, j'ai pensé que c'est évident

par **mathelot** » 07 Juil 2015, 11:44

razel a écrit:Euh, j'ai pensé que c'est évident

je te pose la question car ce n'est pas évident (niveau lycée)

Le calcul du nombre dérivé résout une F.I "

"
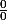
ce qui fait que le numérateur a une limite nulle.
c'est dire que lim f(x)= f(a) quand x tend vers a.

par **zygomatique** » 07 Juil 2015, 12:16

salut

deux méthodes suivant la filière (S ou pas S) de term ...

en S ::

f est dérivable donc f est continue et donc c'est trivial

cas général ::

f est dérivable en a donc au voisinage de a f(a + h) = f(a) + f'(a)h + e(h) avec lim e(h) = 0 quand h --> 0

ou encore en posant x = a + h :: f(x) = f(a) + f'(a)(x - a) + e(x - a)

il suffit alors de faire tendre x vers a ....

réciproque :: évidemment faux en prenant par exemple f(x) = |x| en 0 ....

par **razel** » 07 Juil 2015, 12:46

Merci beaucoup à vous deux

par **razel** » 07 Juil 2015, 13:00

Excuse-moi mathelot, mais je n'ai pas compris ton explication par rapport à mon implication.
Pourquoi le calcul de dérivée résout une F.I?

par **mathelot** » 07 Juil 2015, 13:48

razel a écrit:Excuse-moi mathelot, mais je n'ai pas compris ton explication par rapport à mon implication.
Pourquoi le calcul de dérivée résout une F.I?

l'expression

a une limite.
Comme le dénominateur tend vers zéro, nécessairement le numérateur aussi.
donc lim f(x)=f(a) quand x tend vers a.

par **razel** » 07 Juil 2015, 23:39

Ok, merci mathelot, mais je pense que je n'aurais jamais trouvé la réponse moi-même.
Je sais que ça vient avec le temps, mais pourrais-tu me dire la démarche que tu as suivi pour arriver à ce raisonnement. Désolé de cette question assez bizarre; mais je ne comprends pas comment j'aurais pu avoir cette idée.

par **razel** » 08 Juil 2015, 00:16

Euh...
Pourquoi f(x)=f(a)+f'(a)(x-a)+e(x)(x-a)?
Désolé de mes questions à répétition

par **zygomatique** » 08 Juil 2015, 11:04

par définition de "f est dérivable en a" ... (cours de première)

Dérivation

Dérivation

Qui est en ligne