La dérivation ><'
25 messages
- Page 1 sur 2 - 1, 2
La dérivation ><'
Salut tout le monde ! Alors je vous explique vite fait, j'ai un dm un maths sur la dérivation et je suis bloqué ! :mur:
-> Il faut que je trouve le taux d'accroissement t(h) de l a fonction f(x)=2;)(x) -1 entre 4 et 4+h
j'ai trouvé que c'était égale a [2;)(4+h)-4]/h
->Est-ce qu'il faut que je face de même pour 4+h ?
->Comment je peux faire pour d'après ces réponses démontrer que , pour tout h nombre réel non nuls; t(h)=4/[2;)(4+h)+4] ?
Aidée moi sil vous plait!!!!!! :cry:
-> Il faut que je trouve le taux d'accroissement t(h) de l a fonction f(x)=2;)(x) -1 entre 4 et 4+h
j'ai trouvé que c'était égale a [2;)(4+h)-4]/h
->Est-ce qu'il faut que je face de même pour 4+h ?
->Comment je peux faire pour d'après ces réponses démontrer que , pour tout h nombre réel non nuls; t(h)=4/[2;)(4+h)+4] ?
Aidée moi sil vous plait!!!!!! :cry:
lauw a écrit:Salut tout le monde ! Alors je vous explique vite fait, j'ai un dm un maths sur la dérivation et je suis bloqué ! :mur:
-> Il faut que je trouve le taux d'accroissement t(h) de l a fonction f(x)=2?(x) -1 entre 4 et 4+h
j'ai trouvé que c'était égale a [2?(4+h)-4]/h
->Est-ce qu'il faut que je face de même pour 4+h ?
->Comment je peux faire pour d'après ces réponses démontrer que , pour tout h nombre réel non nuls; t(h)=4/[2?(4+h)+4] ?
Aidée moi sil vous plait!!!!!!
Bonjour,
Je commence d'abord par réécrire ta formule pour qu'elle soit plus lisible. Alors c'est :
Ensuite, il est bon de se rappeler de la formule du taux d'accroissement qui est :
Jusqu'ici, tu es d'accord avec moi ?
Maintenant, on te demande de calculer le taux d'accroissement entre 4 et 4+h. Donc tu calcules
Ensuite pour finir, tu n'auras qu'à remplacer les valeurs que tu trouves dans la formule du taux d'accroissement et simplifier si c'est possible.
J'espère que tu as compris, si ce n'est pas le cas, n'hésite pas à demander, et à exposer ton calcul si tu as des soucis
Allez, bon courage
@lauw
Soit f la fonction définie par f(x)=2;)(x) -1 ( donc définie sur R+ )
Le taux de variation de la fonction f entre 4 et 4+h ( ou entre 4+h et 4 ) est égal à :
( f(4+h) - f(4) ) /(4+h - 4) = ( f(4) - f(4+h) ) /(4 - (4+h)) = ( f(4+h) - f(4) ) /h
 pouvant être positif ou négatif
pouvant être positif ou négatif
ps)
Evite de noter cette fonction=.....) car c'est une fonction de variable
car c'est une fonction de variable  qui dépend de
qui dépend de  et de
et de 
C'est "mieux" de la la noter :=....)
Soit f la fonction définie par f(x)=2;)(x) -1 ( donc définie sur R+ )
Le taux de variation de la fonction f entre 4 et 4+h ( ou entre 4+h et 4 ) est égal à :
( f(4+h) - f(4) ) /(4+h - 4) = ( f(4) - f(4+h) ) /(4 - (4+h)) = ( f(4+h) - f(4) ) /h
ps)
Evite de noter cette fonction
C'est "mieux" de la la noter :
@lauw
soit tu as changé de fonction et tu essaies de calculer un taux de variation entre 3 et 3+h ?
soit tu n'as rien compris aux messages précédents
et si c'est le cas : je te conseille vivement de les relire
ET de les écrire sur une feuille blanche avec un stylo...
(EDIT)
Rappel
Formule permet de calculer le taux de variation d'une fonction entre
entre  et
et 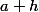
-f(a)}{h})
soit tu as changé de fonction et tu essaies de calculer un taux de variation entre 3 et 3+h ?
soit tu n'as rien compris aux messages précédents
et si c'est le cas : je te conseille vivement de les relire
ET de les écrire sur une feuille blanche avec un stylo...
(EDIT)
Rappel
Formule permet de calculer le taux de variation d'une fonction
@mathelotmathelot a écrit:pas trop d'accord. f et 4 étant des constantes, la notationest correcte.
plus simple que la fonction de trois variables
Vu que c'est une notation ,
tu peux faire comme tu veux du moment que l'on sait sur quelle fonction et où est calculé ce taux
remarque:
Ce taux est une fonction a une seule variable
Bonjour Ptitnoir,
Mon professeur de mathematiques nous a jamais parlé de taux de variation pour ce taux d'accroissement.
Ça m'a même surprise de voir que tu me parlais d'un "autre nom" pour ce taux.
En plus, le taux de variation me rappelle plus des calculs que l'on fait en economie...
Sinon, regardes cette discussion : http://www.maths-forum.com/taux-d-accroissement-taux-variation-123246.php
La preuve que tu n'es pas le seul à penser que ce taux s'appelle "taux de variation", et que d'autres personnes comme moi ne connaissaient pas ce nom avant qu'on nous le dise
Donc au final, j'ai raison ahaha, c'est la taux d'accroissement. Je l'appelerai toujours comme ça.

Mon professeur de mathematiques nous a jamais parlé de taux de variation pour ce taux d'accroissement.
Ça m'a même surprise de voir que tu me parlais d'un "autre nom" pour ce taux.
En plus, le taux de variation me rappelle plus des calculs que l'on fait en economie...
Sinon, regardes cette discussion : http://www.maths-forum.com/taux-d-accroissement-taux-variation-123246.php
La preuve que tu n'es pas le seul à penser que ce taux s'appelle "taux de variation", et que d'autres personnes comme moi ne connaissaient pas ce nom avant qu'on nous le dise
Donc au final, j'ai raison ahaha, c'est la taux d'accroissement. Je l'appelerai toujours comme ça.
@Saccharine
Ces 2 "noms" sont corrects et comme l'a précisé ton ami Kikoo :
le nom 'taux de variation' est peut être plus parlant que le nom "taux d'accroissement" ,
surtout pour les fonctions décroissantes.
Sinon appelle le plutôt le taux d'accroissement de f entre a et a+h que la taux d'accroissement
A+
ps)
Si ce n'est pas trop indiscret : quel âge a ce professeur de maths (ou avait si c'était l'an dernier)
Est ce que d'après toi ce même prof écrit ou écrivait :

ou
 ?
?
Ces 2 "noms" sont corrects et comme l'a précisé ton ami Kikoo :
le nom 'taux de variation' est peut être plus parlant que le nom "taux d'accroissement" ,
surtout pour les fonctions décroissantes.
Sinon appelle le plutôt le taux d'accroissement de f entre a et a+h que la taux d'accroissement
A+
ps)
Si ce n'est pas trop indiscret : quel âge a ce professeur de maths (ou avait si c'était l'an dernier)
Est ce que d'après toi ce même prof écrit ou écrivait :
ou
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
