Dérivation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Live-the-rock
- Membre Naturel
- Messages: 10
- Enregistré le: 12 Avr 2012, 18:37
-
 par Live-the-rock » 10 Nov 2012, 17:49
par Live-the-rock » 10 Nov 2012, 17:49
Bonjour, je dois dériver cette fonction, mais je n'y parviens car je n'arrive pas à détemriner sa forme.
f = (7/2) + (2sinx/cosx) - (4/cosx)
Peut-être en simplifiant ? : f = (7cox+4sinx-8)/2cosx ? donc de forme u/v
Merci d'avance
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 10 Nov 2012, 18:12
par Carpate » 10 Nov 2012, 18:12
Live-the-rock a écrit:Bonjour, je dois dériver cette fonction, mais je n'y parviens car je n'arrive pas à détemriner sa forme.
f = (7/2) + (2sinx/cosx) - (4/cosx)
Peut-être en simplifiant ? : f = (7cox+4sinx-8)/2cosx ? donc de forme u/v
Merci d'avance
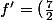'+ 2 (\frac{\sin{x}}{cos{x}})'-4 (\frac{1}{\cos{x}})'=0+ 2 (\frac{\sin{x}}{cos{x}})'-4 (\frac{1}{\cos{x}})')
Même sans lunettes, on voit tout de suite que
')
et
')
sont respectivement de la forme :
}{v'x)})' = \frac{v(x) u'(x)-u(x) v'(x)}{v(x)^2})
et
})'=-\frac{u'(x)}{u(x)^2})
-
Live-the-rock
- Membre Naturel
- Messages: 10
- Enregistré le: 12 Avr 2012, 18:37
-
 par Live-the-rock » 10 Nov 2012, 19:01
par Live-the-rock » 10 Nov 2012, 19:01
Donc f' = (-2cosx/sinx)-(4sinx/cox²) ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 10 Nov 2012, 19:11
par Carpate » 10 Nov 2012, 19:11
Live-the-rock a écrit:Donc f' = (-2cosx/sinx)-(4sinx/cox²) ?
'= \frac{1}{cosx^2})
-
Live-the-rock
- Membre Naturel
- Messages: 10
- Enregistré le: 12 Avr 2012, 18:37
-
 par Live-the-rock » 10 Nov 2012, 19:57
par Live-the-rock » 10 Nov 2012, 19:57
*message supprimé*
-
Live-the-rock
- Membre Naturel
- Messages: 10
- Enregistré le: 12 Avr 2012, 18:37
-
 par Live-the-rock » 10 Nov 2012, 20:06
par Live-the-rock » 10 Nov 2012, 20:06
(

)' =

= 1 +

Je comprends pas où est mon erreur... :/
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 11 Nov 2012, 09:02
par Carpate » 11 Nov 2012, 09:02
Live-the-rock a écrit:(

)' =

= 1 +

Je comprends pas où est mon erreur... :/
Ce n'est pas une erreur mais 2 expressions correctes de la dérivée de tg x
'=\frac{cosx^2+sinx^2}{cosx^2}= \frac{1}{cosx^2}=1 + \frac{sinx^2}{cosx^2})
' = \frac{1}{cosx^2}= 1 +tgx^2)
-
Live-the-rock
- Membre Naturel
- Messages: 10
- Enregistré le: 12 Avr 2012, 18:37
-
 par Live-the-rock » 11 Nov 2012, 14:00
par Live-the-rock » 11 Nov 2012, 14:00
Carpate a écrit:Ce n'est pas une erreur mais 2 expressions correctes de la dérivée de tg x
'=\frac{cosx^2+sinx^2}{cosx^2}= \frac{1}{cosx^2}=1 + \frac{sinx^2}{cosx^2})
' = \frac{1}{cosx^2}= 1 +tgx^2)
A d'accord!
Par contre je ne trouve pas comment passer de 1+tgx^2 à

-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 11 Nov 2012, 14:06
par Carpate » 11 Nov 2012, 14:06
Live-the-rock a écrit:A d'accord!
Par contre je ne trouve pas comment passer de 1+tgx^2 à

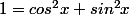
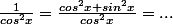
-
Live-the-rock
- Membre Naturel
- Messages: 10
- Enregistré le: 12 Avr 2012, 18:37
-
 par Live-the-rock » 11 Nov 2012, 14:18
par Live-the-rock » 11 Nov 2012, 14:18
Carpate a écrit: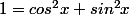
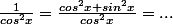
Ah oui... merci beaucoup

Je suis décidement pas une lumière en maths...
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 11 Nov 2012, 14:19
par Carpate » 11 Nov 2012, 14:19
Live-the-rock a écrit:Ah oui... merci beaucoup

Je suis décidement pas une lumière en maths...
Ca vient avec un peu d'entrainement !
-
Live-the-rock
- Membre Naturel
- Messages: 10
- Enregistré le: 12 Avr 2012, 18:37
-
 par Live-the-rock » 11 Nov 2012, 14:25
par Live-the-rock » 11 Nov 2012, 14:25
Carpate a écrit:Ca vient avec un peu d'entrainement !
J'espère

Encore merci!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
