Dérivation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
poiuytre
- Membre Naturel
- Messages: 17
- Enregistré le: 21 Nov 2011, 20:15
-
 par poiuytre » 30 Nov 2011, 16:42
par poiuytre » 30 Nov 2011, 16:42
Bonjour,
je ne vois pas comment faire cette question :
En reprenant la définition et en effectuant un changement de variable judicieux, démonter que:
lim
-f(t-h)}{h})
= f '(t)
h

0
Merci
-
Dlzlogic
- Membre Transcendant
- Messages: 5273
- Enregistré le: 14 Avr 2009, 12:39
-
 par Dlzlogic » 30 Nov 2011, 16:50
par Dlzlogic » 30 Nov 2011, 16:50
Bonjour,
Ben, moi non plus, puisque c'est pour la définition de la dérivée.
-
didou31
- Membre Relatif
- Messages: 230
- Enregistré le: 24 Sep 2008, 16:23
-
 par didou31 » 30 Nov 2011, 18:16
par didou31 » 30 Nov 2011, 18:16
poiuytre a écrit:Bonjour,
je ne vois pas comment faire cette question :
En reprenant la définition et en effectuant un changement de variable judicieux, démonter que:
-f(t-h)}{h}= f '(t))

Merci
Quelle est la définition de la dérivée ?
Si elle est définie comme ceci par exemple :
-f(a)}{x-a}= f '(x))
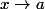
Ca t'inspire ?
-
poiuytre
- Membre Naturel
- Messages: 17
- Enregistré le: 21 Nov 2011, 20:15
-
 par poiuytre » 30 Nov 2011, 18:21
par poiuytre » 30 Nov 2011, 18:21
f est dérivable en x0 si la limite, lorsque h tend vers 0, du rapport
-f(x0-h)}{h})
existe et est finie.
Dans ce cas, la limite du rapport précédent s'appelle le nombre de f en x0.
-
Dlzlogic
- Membre Transcendant
- Messages: 5273
- Enregistré le: 14 Avr 2009, 12:39
-
 par Dlzlogic » 30 Nov 2011, 19:14
par Dlzlogic » 30 Nov 2011, 19:14
@ poluitre
Disons qu'une fonction est dérivable en un point si sa dérivée existe.
Donc, on en est à la définition d'une dérivée, pas une formule, une phrase.
J'ai appris cette définition il y a une cinquantaine d'années, et je m'en souviens encore, c'est comme le vélo, ça ne s'oublie pas.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités