Bonjour, je ne sais pas du tout comment il faut procéder pour mener à bien cette question.
1. Le plan est muni d'un repère (o;i;j)
Une courbe C admet dans le repère une équation du type :
y = ax^3 + bx² + cx + d, où a,b,c,d sont des réels.
Cette courbe :
- est une tangente à la droite d'équation y = -1 au point A d'abscisse 0.
- admet au point B d'abscisse 2/3 une tangente horizontale.
- admet au point C d'abscisse 1 une tangente parallèle à la droite d'équation
y= x + 3
Déterminer les réels a,b,c,d
DERIVATION ; fonction polynôme (T° ES)
13 messages
- Page 1 sur 1
Bonsoir
Important : le coefficient directeur d'une tangente est donné par le nombre dérivé.
Il faut commencer par écrire la fonction dérivée.
La première indication montre que le point A(0,-1) appartient à la cournbe et que f'(0)=0 puisque la tangente en A est parallèle à l'axe des abscisses.
Cela te donne 2 équations d'inconnues a, b, c,d.
La deuxième indication permet d'écrire que f'(2/3) =0 (tangente horizontale)
La troisième indication permet d'écrire quef'(1)=1 car 2 droites parallèles ont même coefficient directeur.
Tu as ainsi un système de 4 équations à 4 inconnues à résoudre.
Important : le coefficient directeur d'une tangente est donné par le nombre dérivé.
Il faut commencer par écrire la fonction dérivée.
La première indication montre que le point A(0,-1) appartient à la cournbe et que f'(0)=0 puisque la tangente en A est parallèle à l'axe des abscisses.
Cela te donne 2 équations d'inconnues a, b, c,d.
La deuxième indication permet d'écrire que f'(2/3) =0 (tangente horizontale)
La troisième indication permet d'écrire quef'(1)=1 car 2 droites parallèles ont même coefficient directeur.
Tu as ainsi un système de 4 équations à 4 inconnues à résoudre.
Bonjour,
il faut traduire chaque phrase par une égalité
"la courbe passe par le point M(truc ; machin)" se traduit par l'égalité
machin = f(truc)
"la tangente au point A d'abscisse bidule a pour cefficient directeur m" se traduit par l'égalité f '(bidule) = m
tu as donc ici
f(x) = ax^3 + bx² + cx + d
f '(x) = 3ax² + 2bx + c
la première phrase se traduit par une double égalité :
la courbe passe par A(0 ; - 1) <=> f(0) = -1 <=> d = -1
la tangente est horizontale <=> f '(0) = 0 <=> c = 0
la deuxième phrase se traduit par une égalité
au point d'abscisse 2/3, la tangente est horizontale <=> f '(2/3) = 0 <=> 3a(2/3)² + 2b(2/3) + c = 0
la troisième phrase se traduit par l'égalité :
au point d'abscisse 1, la tangente a pour coefficient directeur 1 (1 est le coefficient directeur de la droite d'équation y = x + 3) <=> f '(1) = 1 < => ...
Je te laisse finir: tu as un système de 4 équation a 4 inconnues a, b, c, d, qu'il te suffit de résoudre pour trouver l'équation de ta courbe
Bon courage
il faut traduire chaque phrase par une égalité
"la courbe passe par le point M(truc ; machin)" se traduit par l'égalité
machin = f(truc)
"la tangente au point A d'abscisse bidule a pour cefficient directeur m" se traduit par l'égalité f '(bidule) = m
tu as donc ici
f(x) = ax^3 + bx² + cx + d
f '(x) = 3ax² + 2bx + c
la première phrase se traduit par une double égalité :
la courbe passe par A(0 ; - 1) <=> f(0) = -1 <=> d = -1
la tangente est horizontale <=> f '(0) = 0 <=> c = 0
la deuxième phrase se traduit par une égalité
au point d'abscisse 2/3, la tangente est horizontale <=> f '(2/3) = 0 <=> 3a(2/3)² + 2b(2/3) + c = 0
la troisième phrase se traduit par l'égalité :
au point d'abscisse 1, la tangente a pour coefficient directeur 1 (1 est le coefficient directeur de la droite d'équation y = x + 3) <=> f '(1) = 1 < => ...
Je te laisse finir: tu as un système de 4 équation a 4 inconnues a, b, c, d, qu'il te suffit de résoudre pour trouver l'équation de ta courbe
Bon courage
Merci à tous mais ceci n'était que la 1aire des 3 questions de l'exo.
2. Soit f la fonction définie sur R par f(x) = x3 - x²-1.
a) Etudiez les limites de f en + l'infini et en - l'infini.
b) Calculez f'(x) et étudiez les variations de f.
c) Montrez que 1 < a < 2
Donnez, en expliquant la méthode utilisée, une valeur approchée de a à 10-1 près.
Ce que j'ai fait :
a) limite de f en + l'infini : lim x3 = + l'infini ; lim x²= + l'infini donc lim -x² = - l'infini.
Donc je trouve lim f(x) = F.I. Comment la levée ?
limite de f en - l'infini : lim x3 = - l'infini ; lim x² = - l'infini donc lim -x²=+ l'infin
Donc lim f(x) = F.I. Comment la levée ??
b) f'(x) = 3x - 2x
_____________________________
x / - l'infini 0 + l'infini
_____/_______________________
f'(x) / - 0 +
_____/_________________________
f(x) / strict. décr. st. crois.
_____/____________-1__________
Valeur charnière : je remplace 0 dans f'(x); on a 0
Recherche du minimal absolu de la fonction f : je remplace 0 dans f(x) ; on a -1.
c) f est continue sur [0; + l'infini]
f est strict. croiss. sur le m intervalle.D'après le tableau des variations de f
f ([0;+ l'inf.]) = [-1 ;+l'inf.] et 0 appartient à [-1 ; + l'inf]
DONC on peut dire que l'équation f(x) = 0 admet 1 solution a appartenant à [-1; + l'inf.]
d) On calcule les solutions de l'équation f(x)=0 pour trouver la valeur de a sur [0;+ l'inf.]
On résout x3 - x²-1 = 0 Comment faire ??
on doit trouver 1 solution entre 1 et 2
On a 10
Donc a = environ 1.5
Merci d'avance pour votre soutien ; corriger moi si nécessaire
2. Soit f la fonction définie sur R par f(x) = x3 - x²-1.
a) Etudiez les limites de f en + l'infini et en - l'infini.
b) Calculez f'(x) et étudiez les variations de f.
c) Montrez que 1 < a < 2
Donnez, en expliquant la méthode utilisée, une valeur approchée de a à 10-1 près.
Ce que j'ai fait :
a) limite de f en + l'infini : lim x3 = + l'infini ; lim x²= + l'infini donc lim -x² = - l'infini.
Donc je trouve lim f(x) = F.I. Comment la levée ?
limite de f en - l'infini : lim x3 = - l'infini ; lim x² = - l'infini donc lim -x²=+ l'infin
Donc lim f(x) = F.I. Comment la levée ??
b) f'(x) = 3x - 2x
_____________________________
x / - l'infini 0 + l'infini
_____/_______________________
f'(x) / - 0 +
_____/_________________________
f(x) / strict. décr. st. crois.
_____/____________-1__________
Valeur charnière : je remplace 0 dans f'(x); on a 0
Recherche du minimal absolu de la fonction f : je remplace 0 dans f(x) ; on a -1.
c) f est continue sur [0; + l'infini]
f est strict. croiss. sur le m intervalle.D'après le tableau des variations de f
f ([0;+ l'inf.]) = [-1 ;+l'inf.] et 0 appartient à [-1 ; + l'inf]
DONC on peut dire que l'équation f(x) = 0 admet 1 solution a appartenant à [-1; + l'inf.]
d) On calcule les solutions de l'équation f(x)=0 pour trouver la valeur de a sur [0;+ l'inf.]
On résout x3 - x²-1 = 0 Comment faire ??
on doit trouver 1 solution entre 1 et 2
On a 1
Donc a = environ 1.5
Merci d'avance pour votre soutien ; corriger moi si nécessaire
Bonjour, voici je ne sais pas comment procéder pour mener à bien cette dernière question.
3. a) Tracez dans le répère les courbes F et G d'équations respectives y= x² et y=x3-1.
b) Montrez que F et G se coupent en un unique point M dont vous exprimerez les coordonnées en fonction de a. (a= environ 1.5 d'après mes calculs==> Q. 2)
3. a) Tracez dans le répère les courbes F et G d'équations respectives y= x² et y=x3-1.
b) Montrez que F et G se coupent en un unique point M dont vous exprimerez les coordonnées en fonction de a. (a= environ 1.5 d'après mes calculs==> Q. 2)
Bonsoir
Il y a des fautes.
2.a) En - il n'y a pas de forme indéterminée puisque
il n'y a pas de forme indéterminée puisque  et -
et - ont pour limite -
ont pour limite - , f a donc pour limite -
, f a donc pour limite -
Pour lever l'indétermination en + , il faut mettre en facteur le terme de plus haut degré c'est-à-dire
, il faut mettre en facteur le terme de plus haut degré c'est-à-dire  .
.
b)La fonction dérivée est=3x^2-2x=x(3x-2)) Elle s'annule en 0 et en
Elle s'annule en 0 et en 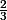 et on peut étudier son signe par un tableau ou par la règle sur le signe du trinôme du second degré.
et on peut étudier son signe par un tableau ou par la règle sur le signe du trinôme du second degré.
c) La question est à revoir étant donné l'erreur dans la fonction dérivée.
d) On ne doit pas résoudre l'équation mais donner une valeur approchée de a avec la calculatrice. (1,4<a<1,5)
3. L'abscisse du point M est solution de l'équation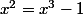 , soit en transposant
, soit en transposant 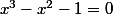 . La solution de cette équation est a donc M apour abscisse a et pour ordonnée
. La solution de cette équation est a donc M apour abscisse a et pour ordonnée 
Il y a des fautes.
2.a) En -
Pour lever l'indétermination en +
b)La fonction dérivée est
c) La question est à revoir étant donné l'erreur dans la fonction dérivée.
d) On ne doit pas résoudre l'équation mais donner une valeur approchée de a avec la calculatrice. (1,4<a<1,5)
3. L'abscisse du point M est solution de l'équation
POur la a) il te suffit de faire un tableau de valeurs pour chacune des fonctions (tableau a la calculatrice ou bien grace a ta tête :marteau: )
Pour la b) on doit resoudre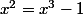 soit
soit
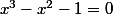
Si on te demande d'exprimer en fonction de a tu ne dois pas le remplacer! :happy2:
Résous cette equation: a est solution donc M a pour abscisse a .
:happy2:
EDit: HAPPY BIRTHDAY TO ME !!! 500EME MESSAGE :ptdr:VIVE LES MEMBRES COMPLEXES LOL
Pour la b) on doit resoudre
Si on te demande d'exprimer en fonction de a tu ne dois pas le remplacer! :happy2:
Résous cette equation: a est solution donc M a pour abscisse a .
:happy2:
EDit: HAPPY BIRTHDAY TO ME !!! 500EME MESSAGE :ptdr:VIVE LES MEMBRES COMPLEXES LOL
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
