Lolrien a écrit:Pour répondre à Lostounet
Pourriez vous m'expliquer pourquoi une fonction qui est continue en un point n'est pas forcèment dérivable, je ne vois pas comment c'est possible.
Pour vérifier si la fonction était continue en 1, j'ai fait la méthode de base.
J'ai calculé f(1), donc avec x²-x-4 et j'ai trouvé -4
Puis j'ai trouvé la limite de (x-5)/x pour x tend vers 1 et avec x>1 et on trouve -4
On en déduit donc que la fonction est continue en 1.
Je ne vois toujours pas pour montrer la dérivabilité en 1, ça me semble étrange.
Quand tu dis qu'une fonction est continue en un point, cela signifie qu'elle est d'un seul tenant autour de se point. Par exemple si je te définis la fonction:
g(x) = 1 si x > 0
g(x) = 0 si x<=0
On voit clairement que cette fonction n'est pas continue en 0 (car elle se "détache" en 0).
Quand tu dis qu'une fonction est dérivable en un point, cela signifie non seulement qu'elle ne se détache pas en ce point, mais aussi qu'elle admet une tangente en ce point ("en gros"). Cela voudrait dire qualitativement qu'elle est "lisse" autour de ce point.
Regarde par exemple cette fonction-là:
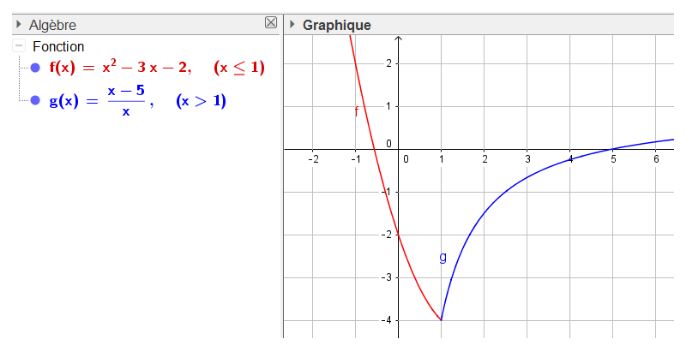
Elle est continue au point 1, mais elle n'a pas de tangente au point 1 (tu vois bien le "pic")... (en fait il y a une "demi-tangente" à gauche de 1 qui est différente de celle de droite de 1.. mais bien entendu ceci est juste quelque chose de qualitatif pour le moment juste pour te donner une idée).
Un autre exemple typique: la fonction valeur absolue, h(x) = |x| qui est continue en 0 mais non dérivable en 0.
Et pour revenir à ton exercice, la méthode consiste à regarder la limite de f'(1 - h) lorsque h tend vers 0 ainsi que f'(1) afin de voir si effectivement la pente de la tangente est la même à droite et à gauche du point 1... c'est le même type de travail que pour la continuité. Il n'y a donc rien d'étrange... si ce n'est que les deux notions sont un peu nouvelles.
PS: Tu l'auras compris, si une fonction est dérivable en un point, c'est qu'elle y est forcément continue ! Car on exige d'elle d'être "lisse"/"douce" en ce point, et donc forcément qu'elle ne devrait pas se détacher brusquement...
Mais la réciproque est fausse, continue n'implique pas dérivable comme le montre cet exercice...
PS2: Mathelot a raison, je trouve que la fonction n'est pas dérivable en 1 non plus. D'ailleurs trace la fonction et tu verras...

