Bonsoir
a^n - b^n=(a-b) [(a^(n-2)+a(n-2)b+...+ab^(n-2)+b^(n-1)]
On me demande de démontrer cette égalité j'ai utilisé la récurrence mais même pour n=2 n'est pas évident
n>=2
a€R
Re: Demonstration par recurence
6 messages
- Page 1 sur 1
Re: Demonstration par recurence
josias a écrit:Bonsoir
a^n - b^n=(a-b) [(a^(n-2)+a(n-2)b+...+ab^(n-2)+b^(n-1)]
On me demande de démontrer cette égalité j'ai utilisé la récurrence mais même pour n=2 n'est pas évident
n>=2
a€R
Bonsoir,
Cette écriture est fausse. Pour
Re: Re: Demonstration par recurence
Bonjour
Oui comme le dit pascal, ça coûte pas cher d'écrire avec le symbole sigma, d'une part et de corriger aussi. Et d'autre part je vois mal pourquoi faire une récurrence la dessus!!
Oui comme le dit pascal, ça coûte pas cher d'écrire avec le symbole sigma, d'une part et de corriger aussi. Et d'autre part je vois mal pourquoi faire une récurrence la dessus!!
Re: Demonstration par recurence
le plus simple
on développe : (a-b) [(a^(n-2)+a(n-2)b+...+ab^(n-2)+b^(n-1)]
en écrivant sur 2 lignes, décalé d'une case
on remarque une somme téléscopique
avec le sigle sigma : la même chose en propre
on développe : (a-b) [(a^(n-2)+a(n-2)b+...+ab^(n-2)+b^(n-1)]
en écrivant sur 2 lignes, décalé d'une case
on remarque une somme téléscopique
avec le sigle sigma : la même chose en propre
Re: Demonstration par recurence
Bonjour;
\overset{n-1}{\underset{k=0}{\Sigma}}a^{n-1-k}b^k=\overset{n-1}{\underset{k=0}{\Sigma}}a^{n-k}b^k-\overset{n-1}{\underset{k=0}{\Sigma}}a^{n-1-k}b^{k+1})
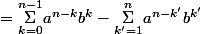
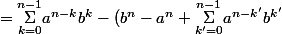)
J'espère que tu peux continuer maintenant et conclure .
En ce qui concerne ta méthode où tu voulais utiliser une récurrence, il serait plus commode de commencer par poser :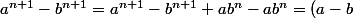b^n + a(a^n-b^n)) avant d'utiliser la propriété de récurrence .
avant d'utiliser la propriété de récurrence .
J'espère que tu peux continuer maintenant et conclure .
En ce qui concerne ta méthode où tu voulais utiliser une récurrence, il serait plus commode de commencer par poser :
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
