Indication : employer une méthode "similaire" à celle de... ton propre défi...Donner les valeurs exactes des solutions de l'équation
Défi "Dinnozzo"
23 messages
- Page 1 sur 2 - 1, 2
Défi "Dinnozzo"
Pour occupper Dinozzo (et éventuellement d'autres...) pendant qu'il donne des indics sur son défi :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Nightmare a écrit:Pourquoi introduire x+1/x ?
Ben, vu que -1 est une racine évidente, il nous suffirait donc de résoudre
Or comme c'est un polynôme à coefficients symétriques, et comme 0 n'est pas solution, on peut se permettre de diviser le tout par
On aura donc :
Là, le changement de variable que j'ai introduit saute aux yeux
à partir de là je sais faire,
pour X = 0
f(X)=+7 qui n'est pas nul, donc -3/X est solution,ou 1/X est solution, ou -7x1/X est solution ou, le premier qui donne une règle comme celle de Ben gagne ma considération,
c'est pénible d'apprendre les solutions des polynomes uniquement sur des exemples, et en plus, plus tu fais d'exos et plus cela fait de solutions qui ont déjà marché à essayer ...
PS: désolé je suis en retard , je viens de la page 1
pour X = 0
f(X)=+7 qui n'est pas nul, donc -3/X est solution,ou 1/X est solution, ou -7x1/X est solution ou, le premier qui donne une règle comme celle de Ben gagne ma considération,
c'est pénible d'apprendre les solutions des polynomes uniquement sur des exemples, et en plus, plus tu fais d'exos et plus cela fait de solutions qui ont déjà marché à essayer ...
PS: désolé je suis en retard , je viens de la page 1
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Une remarque, le polynôme  est dit symétrique ses coefficient sont disposés de manière symétrique : 1 ; -5 ; 3 ; 3 ; -5 ; 1. Il en est de même pour
est dit symétrique ses coefficient sont disposés de manière symétrique : 1 ; -5 ; 3 ; 3 ; -5 ; 1. Il en est de même pour  .
.
Cela peu avoir une certaine importance.
Il me semble même que si un polynôme est symétrique alors "ma méthode" explicitée dans mon défi fonctionne à coup sûr.
On remarque qu'il y a une racine évidente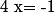 , car
, car =0) . Il existe donc un polynôme
. Il existe donc un polynôme  de degré
de degré 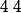 tel que, pour tout
tel que, pour tout  réel :
réel :
=(x+1)f(x))
avec=x^4+ax^3+bx^2+cx+d)
Pour tout :
:
=(x+1)f(x)=(x+1)(x^4+ax^3+bx^2+cx+d))
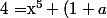x^4+(a+b)x^3+(b+c)x^2+(c+d)x+d)
Par identification, cela équivaut à :

d'où

Ainsi=x^4-6x^3+9x^2-9x+1)
On résous alors=0) .
.
\neq 0) , donc
, donc 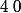 n'est pas racine de
n'est pas racine de  . On peut par conséquent supposer que si
. On peut par conséquent supposer que si  est racine de
est racine de  alors
alors 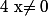 .
.
Soit un réel non nul.
un réel non nul.
Si est racine de
est racine de  alors
alors =0)
(ce qui équivaut à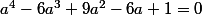.)
=\frac{1}{a^4}+\frac{-6}{a^3}+\frac{9}{a^2}+\frac{-6}{a}+1)
}{a^4})
Or=0) si
si 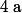 est racine de
est racine de  , par conséquent
, par conséquent =0) .
.
En conclusion, si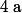 est racine de
est racine de  alors
alors  l'est également.
l'est également.
Posons :
On a donc : .
.
Pour tout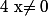 :
:
}{x^2}=x^2-6x+9+\frac{-6}{x}+\frac{1}{x^2})

Déterminons alors les racines de ce trinôme d'inconnue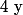 :
:
 donc
donc


Or
On résous donc : [1] et
[1] et  [2]
[2]
Et au final on a donc pour solutions :
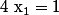 ;
; ^2-4}}{2}) ;
; ^2-4}}{2})
Waouh, c'est fini, ça m'a pris un peu tout l'aprem :ptdr:
Cela peu avoir une certaine importance.
Il me semble même que si un polynôme est symétrique alors "ma méthode" explicitée dans mon défi fonctionne à coup sûr.
On remarque qu'il y a une racine évidente
avec
Pour tout
Par identification, cela équivaut à :
d'où
Ainsi
On résous alors
Soit
Si
(ce qui équivaut à
Or
En conclusion, si
Posons :
On a donc :
Pour tout
Déterminons alors les racines de ce trinôme d'inconnue
Or
On résous donc :
Et au final on a donc pour solutions :
Waouh, c'est fini, ça m'a pris un peu tout l'aprem :ptdr:
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
