Concours Général Maths 2023

[Arc]

Bonjour/bonsoir j'espère que vous allez bien.
Je n'arrive pas à résoudre la question 11 Partie C de l'exercice 2, ni à comprendre le raisonnement du corrigé...
pouvez-vous m'aider ?
Merci d'avance

sujet et corrigé: (2023)
https://www.freemaths.fr/annales-compos ... nnees/2023

[Ben314]

Salut,
C'est ce qu'on appelle souvent "le principe des tiroirs" :
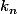
Pour tout entier , vu que est vraiment sympathique il existe un indice (avec ) tel que :

La suite ne peut prendre qu'un nombre fini de valeurs (à savoir 1,2,...,) mais elle contient une infinité de termes donc il y a forcément une certaine valeur qu'elle prend une infinité de fois (*). Si on note cette valeur (avec ) prise une infinité de fois, il y a donc une infinité d'entiers tels que l'on ait :

Ce qui, vu que les suites sont supposées convergentes, est suffisant pour en conclure que

- Attention à l'inégalité stricte qui devient large lors du passage à la limite.
- Attention aussi au fait qu'on ne pouvait évidement pas faire ce type de déduction avec la première série d'inégalité vu que l'endroit du changement de signe dans les coefficients dépendait du polynôme.
Et sinon, les inégalités ci dessus implique clairement que le polynôme est soit vraiment sympathique (si un des coeff. d'indice a une limite non nulle), soit initialement sympathique (si tout les coeff. d'indice tendent vers 0)

(*) Par exemple, s'il n'y avait que 17 termes de la suite égaux à 1, que 23 égaux à 2, que 45 égaux à 3, . . ., que 99 égaux à alors la suite aurais 17+23+45+...+99 termes. Or elle a une infinité de termes . . .

[Arc]

Je comprends, merci beaucoup pour votre aide
Une autre question si possible:
Concernant l'exercice 1, question 4,
Dans la page 4 du corrigé, comment ont-ils fait pour établir la relation Rk ? est-ce à travers une conjecture ?
où est-ce qu'il y a un théorème/astuce qui permet de l'établir (étant donné les écritures de Up selon p impair et pair ) ?
merci beaucoup

[Ben314]

Dans la correction, ce qu'il prennent comme proposition à démontrer par récurrence, c'est lié au formules déjà démontrées qui disent que, si on connait la valeur de , alors on peut en déduire celles de et de .
Donc, connaissant la valeur de tu peut en déduire celle de et de .
Connaissant la valeur de et tu peut en déduire celle de , , et .
Connaissant les valeurs de tu peut en déduire celle de .
etc . . .

Mais, bon, on pouvait aussi faire une bête récurrence forte, ça marchait tout aussi bien.

EDIT : Sinon, je viens de regarder les deux dernières questions et la façon dont ils procèdent dans la correction me semble bien compliqué vu qu'on peut parfaitement faire les deux en même temps en faisant une récurrence (forte) sur pour montrer qu'il existe un unique entier tel que .(la seule chose à utiliser, c'est le fait que les termes d'indice pair sont tous >1 et que ceux d'indice impair >=3 sont tous <1)