Bonsoir à tous,
Sincèrement, je rencontre d'énormes difficultés quand il s'agit de savoir si un ensemble est soit ouvert , soit non ouvert.
En fait ce qui me fatigue le plus est que je n'ai pas d'indice pour savoir si l'ensemble est ouvert ou n'est pas ouvert, et si ce n'est pas ouvert comment trouver le contre-exemple approprié. Et je n'arrive construire les problèmes dans mon esprit.
Par exemple , on donne A= {(x,y) ∈ R²: 1<x<3, y=0 }
Il est question de savoir si A est fermé/ouvert.
*voyons si A est fermé.
Soit (xₙ,yₙ) =( 1+1/n, 0) , ∀ n ∈ N, (xₙ,yₙ) ∈ A.
par passage à la limite on a lim (xₙ,yₙ) = (1,0) qd x tens vers +∞. comme (1,0) ∉ A donc A n' est pas un fermé.
*Voyons si A est un ouvert.
Là je ne vois pas comment faire.
Merci pour votre aide!
Comment montrer qu'un ensemble est ouvert / n'est pas ouvert
11 messages
- Page 1 sur 1
Re: Comment montrer qu'un ensemble est ouvert / n'est pas ou
Intuitivement :
Un ensemble ouvert est un ensemble stable par petites perturbations. (penser à un intervalle ouvert)
Un ensemble fermé est un ensemble stable par passage à la limite (penser à un intervalle fermé).
En espérant que cela t'aide
Un ensemble ouvert est un ensemble stable par petites perturbations. (penser à un intervalle ouvert)
Un ensemble fermé est un ensemble stable par passage à la limite (penser à un intervalle fermé).
En espérant que cela t'aide
Re: Comment montrer qu'un ensemble est ouvert / n'est pas ou
Il est facile de faire un dessin de ton A. L'as-tu fait ?
Re: Comment montrer qu'un ensemble est ouvert / n'est pas ou
GaBuZoMeu a écrit:Il est facile de faire un dessin de ton A. L'as-tu fait ?
Oui oui . quand je prend un point (x,y) de R², je choisis r = min ( 1-x , 3-x ).
Maintenant il reste à savoir si tous les points de la boule B((x,y),r) sont dans A .
Mais en travaillant ainsi, c'est pour montrer que A est un ouvert, pour rien ne me dit ue c'est vraiment ouvert( et c'est ce qui me dérange ), je travaille sans savoir ce qui m'attend.
Re: Comment montrer qu'un ensemble est ouvert / n'est pas ou
Sinon, pour montrer qu'une partie est un ouvert dans R^2, tu peux montrer que son complémentaire est fermé en utilisant la caractérisation séquentielle des fermés sur le complémentaire de A (même si ce n'est pas la méthode la plus élégante)
Ici, A n'est pas un ouvert de R^2
Ici, A n'est pas un ouvert de R^2
Modifié en dernier par LB2 le 07 Oct 2019, 18:47, modifié 2 fois.
Re: Comment montrer qu'un ensemble est ouvert / n'est pas ou
EDIT : Décidément je dis beaucoup de bêtises ce soir...
Modifié en dernier par LB2 le 07 Oct 2019, 18:47, modifié 1 fois.
Re: Comment montrer qu'un ensemble est ouvert / n'est pas ou
Je veux savoir pourquoi c'est faux. Car un ensemble A est ouvert si pour tout x appartenant à A , il existe un ouvert qui contient x contenu dans A, autrement dit, il existe un réel r strictement positif tel que B(x,r) soit inclut dans A.
Re: Comment montrer qu'un ensemble est ouvert / n'est pas ou
Au temps pour moi, ta définition est tout à fait juste, j'ai dit une grosse bêtise.
Ce qu'il faut préciser en revanche : A n'est pas ouvert dans R^2.
En effet, la notion d'ouvert/fermé dépend de l'espace topologique ambiant.
Ce que je voulais dire, c'est que A est ouvert dans A (tautologie), et également ouvert dans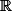 X
X 
En revenant à ma définition intuitive de départ, il est facile de voir que A n'est pas stable par de petites perturbations dans la direction de l'axe des ordonnées (en fait, dans toute direction qui n'est pas celle de l'axe des abscisses). Donc A n'est pas ouvert dans R^2. Attention, cette heuristique ne remplace pas une preuve rigoureuse avec les voisinages ou les boules ouvertes.
Ce qu'il faut préciser en revanche : A n'est pas ouvert dans R^2.
En effet, la notion d'ouvert/fermé dépend de l'espace topologique ambiant.
Ce que je voulais dire, c'est que A est ouvert dans A (tautologie), et également ouvert dans
En revenant à ma définition intuitive de départ, il est facile de voir que A n'est pas stable par de petites perturbations dans la direction de l'axe des ordonnées (en fait, dans toute direction qui n'est pas celle de l'axe des abscisses). Donc A n'est pas ouvert dans R^2. Attention, cette heuristique ne remplace pas une preuve rigoureuse avec les voisinages ou les boules ouvertes.
Re: Comment montrer qu'un ensemble est ouvert / n'est pas ou
Salut !
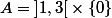 ; je te rappelle que
; je te rappelle que  est ouvert si quel que soit le point
est ouvert si quel que soit le point ) dans
dans  , on peut toujours trouver une boule centrée en
, on peut toujours trouver une boule centrée en ) contenue dans
contenue dans  , ce qui revient à dire que l'on peut toujours trouver un rayon
, ce qui revient à dire que l'on peut toujours trouver un rayon 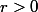 , tel que
, tel que ,r)\subset A) . Considère par exemple le point
. Considère par exemple le point ) . Quel que soit le rayon
. Quel que soit le rayon 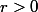 , on peut trouver des points dans
, on peut trouver des points dans ,r)) qui n'appartiennent pas à
qui n'appartiennent pas à  (par exemple le point
(par exemple le point ) ).
).
Ou encore, on a toujours l'inclusion \subset A) . Or par définition, l'intérieur
. Or par définition, l'intérieur ) de
de  est le plus grand ouvert contenu dans
est le plus grand ouvert contenu dans  donc si
donc si  est ouvert alors
est ouvert alors =A) . Or
. Or = \emptyset) donc cela impliquerait que
donc cela impliquerait que 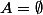 , ce qui n'est pas le cas.
, ce qui n'est pas le cas.
Ou encore, on a toujours l'inclusion
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Comment montrer qu'un ensemble est ouvert / n'est pas ou
je comprend parfaitement ton raisonnement.capitaine nuggets a écrit:Salut !; je te rappelle que
est ouvert si quel que soit le point
dans
, on peut toujours trouver une boule centrée en
contenue dans
, ce qui revient à dire que l'on peut toujours trouver un rayon
, tel que
. Considère par exemple le point
. Quel que soit le rayon
, on peut trouver des points dans
qui n'appartiennent pas à
(par exemple le point
).
Ou encore, on a toujours l'inclusion. Or par définition, l'intérieur
de
est le plus grand ouvert contenu dans
donc si
est ouvert alors
. Or
donc cela impliquerait que
, ce qui n'est pas le cas
Excusez moi mais je veux savoir comment vous avez fait pour trouver int (A)=∅ . Tel que je comprend la chose , puisque A est le produit cartésien de deux ensembles, on fait int ]1,3[ x int ∅ je veux savoir si c'est ce que vous avez fait .
Re: Comment montrer qu'un ensemble est ouvert / n'est pas ou
Merci pour vos reponses jusqu'à maintenant.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
