Montrer qu'un ensemble est ouvert
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Georges10
- Membre Relatif
- Messages: 359
- Enregistré le: 23 Avr 2018, 12:01
-
 par Georges10 » 02 Oct 2019, 11:34
par Georges10 » 02 Oct 2019, 11:34
Bonjour à tous, svp j'aimerais m'assurer d'une chose .
Dans cet exercice,

. Mon problème concerne le C. Il est dit que C n'est pas ouvert.
Ce que j'aimerais savoir c'est sur quelle distance se base t-on pour dire que (0,1+ε) ∈ à toute boule contenant (0,1).
Merci d'avance !
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 02 Oct 2019, 11:55
par Tuvasbien » 02 Oct 2019, 11:55
Je pense que l'énoncé considère que
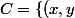\in\mathbb{R}^2\ |\ |x|<1 \text{ ou } |y|<1\})
ce qui n'est pas le cas vu comment il a été définie. Si on considère que
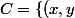\in\mathbb{R}^2\ |\ |x|<1 \text{ et } |y|<1\})
, alors ce n'est pas un fermé puisque si
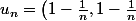)
alors
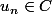
pour tout

mais sa limite
\notin C)
. C'est par contre un ouvert puisque si
\in C)
, alors la boule de centre
)
et de rayon
)
est incluse dans

.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 02 Oct 2019, 11:58
par capitaine nuggets » 02 Oct 2019, 11:58
Salut !
A priori, on parle de la norme euclidienne usuelle (de toute façon, cela importe peu, tu peux choisir n'importe laquelle puisqu'en dimension finie toutes les normes sont équivalentes). Quel que soit le rayon
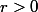
que l'on se donne, on peut toujours trouver un point de
,r))
qui n'appartient pas à

(prendre par exemple le point
)
). Donc

n'est pas ouvert.

-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 02 Oct 2019, 12:23
par LB2 » 02 Oct 2019, 12:23
Attention à la formulation très trompeuse de l'exercice : ouvert et fermé ne sont pas deux notions opposées en maths.
On peut très bien être (dans des espaces bien choisis) à la fois ouvert et fermé, ou ni ouvert ni fermé...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
 . Mon problème concerne le C. Il est dit que C n'est pas ouvert.
. Mon problème concerne le C. Il est dit que C n'est pas ouvert. . Mon problème concerne le C. Il est dit que C n'est pas ouvert.
. Mon problème concerne le C. Il est dit que C n'est pas ouvert.