DM besoin d'aide
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Milog
- Membre Naturel
- Messages: 33
- Enregistré le: 27 Jan 2010, 23:49
-
 par Milog » 28 Jan 2010, 00:00
par Milog » 28 Jan 2010, 00:00
Bonjour,
je viens a vous pour vous demander de l'aide pour faire mon DM de maths, il ne me reste plus que 36h :p
voila la question:
Soit f la fonction définie sur [0:+ [ par f(x) =
[ par f(x) = 
Démontrer que f n'est pas dérivable en 0voila
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 28 Jan 2010, 09:44
par Sylviel » 28 Jan 2010, 09:44
et bien je te suggère de reprendre la définition de la dérivabilité en 0 (tu sais celle avec les limites...) et de calculer la limite.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
massengo
- Membre Naturel
- Messages: 23
- Enregistré le: 26 Jan 2010, 16:31
-
 par massengo » 28 Jan 2010, 09:49
par massengo » 28 Jan 2010, 09:49
On te demande simplement de monter que la dérivée de f n'est pas définie en 0. Alors f '(x)= 1/2racine(x), on voit bien que f '(x) existe que si x>0. Donc la dérivée de f n'existe pas en 0 ou f n'est pas derivable en 0
-
Milog
- Membre Naturel
- Messages: 33
- Enregistré le: 27 Jan 2010, 23:49
-
 par Milog » 28 Jan 2010, 11:33
par Milog » 28 Jan 2010, 11:33
Je vois bien que c'ets dérivable que si X est différent de 0 mais j'ai besoin de le démontrer !
et pareil pour la valeur absolue de X.
j'arrive pas trop a comprendre quels démarches faire pour Démontrer.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 28 Jan 2010, 11:49
par Ben314 » 28 Jan 2010, 11:49
Salut,
As tu suivi les indications de Sylviel ? (celle de massengo ne sont pas trés correctes...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Milog
- Membre Naturel
- Messages: 33
- Enregistré le: 27 Jan 2010, 23:49
-
 par Milog » 28 Jan 2010, 12:04
par Milog » 28 Jan 2010, 12:04
c'est ce que je suis entrain d'essayer mais je me suis jamais entrainé sur ça donc j'ai un peu de mal!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 28 Jan 2010, 12:23
par Ben314 » 28 Jan 2010, 12:23
Tu doit avoir dans ton cours la définition de ce que l'on appelle "le nombre dérivé d'une fonction f au point a" (c'est la limite du taux d'accroissement...)
Tu n'as qu'à appliquer cette définition à la fonction
=\sqrt{x})
en prenant le point

: tu va trouver une limite trés simple...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Milog
- Membre Naturel
- Messages: 33
- Enregistré le: 27 Jan 2010, 23:49
-
 par Milog » 28 Jan 2010, 12:23
par Milog » 28 Jan 2010, 12:23
En calculant la dérivé de racine de x en 0 je trouve:
Racine de h sur h
et après je peux plus rien faire !
Si je fais lim lorsque h tend vers 0 ça serait une grosse erreur.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 28 Jan 2010, 12:25
par Ben314 » 28 Jan 2010, 12:25
Milog a écrit:En calculant la dérivé de racine de x en 0 je trouve:
Racine de h sur h
et après je peux plus rien faire !
Aprés, la définition te dit que tu doit étudier la limite de cette quantité lorsque h tend vers 0.
Indication : pour h positif, on peut écrire
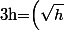^2)
..
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Milog
- Membre Naturel
- Messages: 33
- Enregistré le: 27 Jan 2010, 23:49
-
 par Milog » 28 Jan 2010, 12:34
par Milog » 28 Jan 2010, 12:34
Même quand je continue en disant :
lorsque h>0 on peut écrire: racine de h sur (racine de h)²
en siplifiant je trouve 1 sur racine de h
j'arrive pas a comprendre ce que je dois trouver, je dois montrer que c'est impossible d'avoir le dérivé de 0 pour f(x) = racine carré de x
qu'est ce que je dois montrer a la fin de la démonstration pour dire que c'est impossible?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 28 Jan 2010, 12:51
par Ben314 » 28 Jan 2010, 12:51
Milog a écrit:lorsque h>0 on peut écrire: racine de h sur (racine de h)²
en siplifiant je trouve 1 sur racine de h
Quelle est la limite de

lorsque h tend vers 0 ?
Si cette limite existe et vaut un nombre réel L, cela signifie (c'est la définition) que la fonction f est dérivable en a=0 et que le nombre dérivé est L.
Sinon, cela signifie que f n'est pas dérivable en a=0.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 28 Jan 2010, 15:27
par Sylviel » 28 Jan 2010, 15:27
Plus haut tu parlais aussi de la fonction valeur absolue. Là le problème est différent : il y a "deux manières" d'approcher zéro (par la gauche ou par la droite) et qu'elle donnent de résultats différents pour la limite du taux de variation. Par conséquent il n'y a pas de limite unique donc de valeur de la dérivée.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Milog
- Membre Naturel
- Messages: 33
- Enregistré le: 27 Jan 2010, 23:49
-
 par Milog » 28 Jan 2010, 18:39
par Milog » 28 Jan 2010, 18:39
s'il vous plait personne sait ce qu'il faut faire?
je dois rendre mon dm demain :p
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 28 Jan 2010, 18:44
par Sylviel » 28 Jan 2010, 18:44
précise ta question car on t'as déjà fournit des éléments de réponses...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Milog
- Membre Naturel
- Messages: 33
- Enregistré le: 27 Jan 2010, 23:49
-
 par Milog » 28 Jan 2010, 20:02
par Milog » 28 Jan 2010, 20:02
dsl j'avais pas remarqué la deuxième page dans le sujet :briques:
-
Milog
- Membre Naturel
- Messages: 33
- Enregistré le: 27 Jan 2010, 23:49
-
 par Milog » 28 Jan 2010, 20:05
par Milog » 28 Jan 2010, 20:05
Sylviel a écrit:Plus haut tu parlais aussi de la fonction valeur absolue. Là le problème est différent : il y a "deux manières" d'approcher zéro (par la gauche ou par la droite) et qu'elle donnent de résultats différents pour la limite du taux de variation. Par conséquent il n'y a pas de limite unique donc de valeur de la dérivée.
si ça ne te dérange pas est ce que tu peux m'expliquer un peux plus parce j'arrive pas a tous saisir.
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 28 Jan 2010, 20:16
par Sylviel » 28 Jan 2010, 20:16
ben quelle est la limite de ton taux de variation si tu te contente de t'approcher de 0 par les valeurs positives ?
Quelle est la limite ... par les valeurs négatives ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Milog
- Membre Naturel
- Messages: 33
- Enregistré le: 27 Jan 2010, 23:49
-
 par Milog » 28 Jan 2010, 20:22
par Milog » 28 Jan 2010, 20:22
tu me parle de taux de variation mais je ne suis pas sur de l'avoir fait, j(ai fait une recherche dans google et je trouvé cette formule;

est ce que tu parle de cette formule quand tu dis taux de variation?
(si c'est le cas je peux pas le faire car je n'ai jamais appris cette formule.
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 28 Jan 2010, 20:23
par Sylviel » 28 Jan 2010, 20:23
c'est quoi ta définition de la dérivée ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Milog
- Membre Naturel
- Messages: 33
- Enregistré le: 27 Jan 2010, 23:49
-
 par Milog » 28 Jan 2010, 20:24
par Milog » 28 Jan 2010, 20:24
f(a) = f(a + h) - f(a) sur h
...
valeur absolue de h sur h!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
 [ par f(x) =
[ par f(x) = 
 [ par f(x) =
[ par f(x) = 