Bonjour,
Je suis entrain de faire un exercice sur les approximation affine & je bloque sur une question... J'aurais donc besoin d'aide, n'ayant pas mes cours à portée de main! Bien sur, un developpé :)
Donc voila :
f la fonction définie sur ]-~;2] par f(x) = racine(4 -2x)
1) Définir l'approximation affine au voisinage de 0
En déduire une valeur approchée de racine(3,998)
Merci d'avance & bonne journée :)
Approximation affine
13 messages
- Page 1 sur 1
JAEGARN a écrit:Bonjour,
Je suis entrain de faire un exercice sur les approximation affine & je bloque sur une question... J'aurais donc besoin d'aide, n'ayant pas mes cours à portée de main! Bien sur, un developpé
Donc voila :
f la fonction définie sur ]-~;2] par f(x) = racine(4 -2x)
1) Définir l'approximation affine au voisinage de 0
En déduire une valeur approchée de racine(3,998)
Merci d'avance & bonne journée
Cela ressemble fortement à de la différentiabilité. Regarde cette page : http://euler.ac-versailles.fr/baseeuler/lexique/notion.jsp?id=20
et on attend tes propositions... :id:
En fait, il faut que tu comprennes que l'on peut approcher une fonction par sa tangente au voisinage du point considéré.
) est approximé, dans un voisinage de
est approximé, dans un voisinage de  , par l'expression de la tangente à la courbe
, par l'expression de la tangente à la courbe  en
en  .
.
La tangente à la courbe en
en  est la droite affine d'équation
est la droite affine d'équation 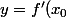(x-x_0)+f(x_0)) à condition que
à condition que  soit dérivable en
soit dérivable en  .
.
On note\sim_{x_0}=f^\prime (x_0)(x-x_0)+f(x_0)) .
.
Applique cette notion de cours de 1ère S à ton problème.
J'attends ta réponse...
La tangente à la courbe
On note
Applique cette notion de cours de 1ère S à ton problème.
J'attends ta réponse...
JAEGARN a écrit:Bonjour,
Je suis entrain de faire un exercice sur les approximation affine & je bloque sur une question... J'aurais donc besoin d'aide, n'ayant pas mes cours à portée de main! Bien sur, un developpé
Donc voila :
f la fonction définie sur ]-~;2] par f(x) = racine(4 -2x)
1) Définir l'approximation affine au voisinage de 0
En déduire une valeur approchée de racine(3,998)
Merci d'avance & bonne journée
En fait, il faut que tu comprennes que l'on peut approcher une fonction par sa tangente au voisinage du point considéré.
) est approximé, dans un voisinage de
est approximé, dans un voisinage de  , par l'expression de la tangente à la courbe
, par l'expression de la tangente à la courbe  en
en  .
.
La tangente à la courbe en
en  est la droite affine d'équation
est la droite affine d'équation 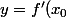(x-x_0)+f(x_0)) à condition que
à condition que  soit dérivable en
soit dérivable en  .
.
L'approximation se note\sim_{x_0}f^\prime (x_0)(x-x_0)+f(x_0)) .
.
Applique cette notion de cours de 1ère S à ton problème.
J'attends ta réponse...
La tangente à la courbe
L'approximation se note
Applique cette notion de cours de 1ère S à ton problème.
J'attends ta réponse...
JAEGARN a écrit:Bonjour,
Je suis entrain de faire un exercice sur les approximation affine & je bloque sur une question... J'aurais donc besoin d'aide, n'ayant pas mes cours à portée de main! Bien sur, un developpé
Donc voila :
f la fonction définie sur ]-~;2] par f(x) = racine(4 -2x)
1) Définir l'approximation affine au voisinage de 0
En déduire une valeur approchée de racine(3,998)
Merci d'avance & bonne journée
Fanatic a écrit:En fait, il faut que tu comprennes que l'on peut approcher une fonction par sa tangente au voisinage du point considéré.est approximé, dans un voisinage de
, par l'expression de la tangente à la courbe
en
.
La tangente à la courbeen
est la droite affine d'équation
à condition que
soit dérivable en
.
On note.
Applique cette notion de cours de 1ère S à ton problème.
J'attends ta réponse...
Je suis peut-être lourd avec mes rectifications LaTeX, surtout que là, ça va servir à rien (donc je vais me faire prévenir par le modo).
Un truc en dessous d'un autre, ça s'écrit :
Désolé encore :triste: !
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

