Application d'I.A.F

par **sue** » 11 Déc 2006, 13:56

salut !

on a

et

je veux démontrer que :

moi je trouve :

je vois pas comment appliquer I.A.F :briques:

merci pour votre aide :we:

par **maturin** » 11 Déc 2006, 14:33

alors déjà je touve aps pareil que toi pour f'a(x) j'ai pas le facteur 2 en bas.

Sinon je te conseille plutot d'écrire f'a(u) histoire d'éviter d'avoir des x qui veulent dirent 2 choses.

Enfin pour l'inégalité elle est un peu bizarre vu la simplicité de la dérivée.

Enfin j'ai pas fait les calculs mais tu n'as qu'à montrer que le membre de gauche est un minorant de la dérivée, et le membre de droite un majorant (avec le facteur (x-a) à enlever)

par **sue** » 11 Déc 2006, 14:56

oui merci , j'ai refait mes calculs et je trouve bien

mais comme ça on a :

et bien evidemment on a

donc ça marche pas :hein:

par **maturin** » 11 Déc 2006, 14:59

je suis d'accord avec toi.

enfin ça démontre

vu que tu as x<a

mais pour l'autre ça aurait plutot tendance à prouver le contraire...
y aurait pas d'erruer d'énoncé par hasard ?

par **maturin** » 11 Déc 2006, 15:07

bon j'ai essayé avec un exemple et ça a bien l'air vrai aussi pour cette inégalité.

par **sue** » 11 Déc 2006, 15:12

ben je crois qu'effectivement il y a une erreur d'énoncé , mais pour le moment c tt ce que j'ai , en tt cas je poserai la question à mon prof ..
en fait , ce qui est plus étrange encore c'est qu'aprés on me demande d'étudier la dérivabillité de

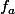
sur [0,a] or avant d'appliquer l'I.A.F il faut vérifier cette condition non ?

par **sue** » 11 Déc 2006, 15:14

bon j'ai essayé avec un exemple et ça a bien l'air vrai aussi pour cette inégalité.

dans ce cas il me semble qu'il y a une contradiction non?:hein:

par **maturin** » 11 Déc 2006, 15:23

bon alors je comprends pas tout e j'ai pas le temps de faire bcp plus de calcul, en fait j'ai fait un exemple avec a=5 et ça a l'air de marcher mais en meme temps je comprends pas pourquoi vu la gueule de la formule et de ce qu'on a calculé.

Je vais creuser car ce point m'interpèle mais pas tout de suite...
Si tu trouves d'ici là.

Et effectivement pour l'IAF il faut bien avoir la dérivabilité...

par **sue** » 11 Déc 2006, 15:30

ok merci maturin !
je chercherai encore car cela m'intirgue :hum:

par **sue** » 11 Déc 2006, 20:05

bon bon je trouve plus rien moi :triste: j'ai essayé une autre valeur et je trouve que l'inégalité marche bien pourtant quand on applique I.A.F ça marche pas :hum:

si qqn d'autre aura une idée , je vois que maturin et déconnecté ...

Application d'I.A.F

application d'I.A.F

Qui est en ligne