Dm 1er S

[ayana77]

j'ai un probléme sur un exercice sur les suites et je n'y arrive pas du tout pouriez vous m'aidez merci d'avance. Voici l'énoncé

On considére n sphère concentriques de centre O et de rayon respectifs 1,2,3,...,n,n+1.

1) Déterminer le volume V de la plus grosse sphère ( ou boule) extérieur.

2)On appelle Vk le volume délimité par les sphères de rayon k et de rayon k+1.

a) Montrer que Vk= 4/3 pi (3k² + 3k + 1).
b) Exprimer V en fonction de Vk.

3) En déduire que (n+1) au cube =3(1²+2²+3²+...+n²) + 3(1+2+3+...+n) +n+1

4) Prouvez que 1²+2²+3²+...+n²= [n(n+1)(2n+1)]/ 6

merci beaucoup pour votre aide car je n'y arrive vraiment pas même en m'aidant de mon cour.

[Daragon geoffrey]

slt
le volume d'une sphere est donné par : V=(4/3)pir^3 où est la rayon, on associe alor pour tt r réel la fct défini par f(r)=(4/3)pir^3 dérivable sur et de dérivée f'=4pir^2, positive ou nulle (si r=0) pour tt r, trace alor le tableau de variation et calcule les limites, tu constates que lim f = + inf (en + et - l'infini), on ne s'interesse qu'à la partie positive des réels, donc la sphère de plus grand volume est ossi celle de plus grand rayon, cad de rayon k+1 !
pour la 2 : je note V' ce que toi tu appelles Vk, par définition, V'=V(k+1)-Vk où Vk est le volume de la sphère de rayon k et on obtient, aprè simplification : V'=(4/3)pi[3k^2 +3k+1]
pour la 3 : on a simplement V=V'+Vk=V(k+1)=(4/3)pi(k+1)^3, qui est ossi la réponse à la première question ! pour la question suivante exploite la formule précédente et enfin pour la dernière, procède par récurrence : tu poses
Pn : 1+4+8+...+n^2 = [n(n+1)(2n+1)]/6 or P1 par définition vaut 1, et daprè la formule explicite suggérée par l'énoncé, on obtient ossi 1 donc P1 est vraie. maintenant on suggère Pn vrai pour tt n sup ou égal à 1 et on démontre que Pn est encore vraie o rang n+1 : or on a 1+4+8+...+n^2 +(n+1)^2 =[n(n+1)(2n+1)]/6 +(n+1)^2=[(n+1)(n+2)(2n+3)]/6 qui coincide avec ce quon doit trouver en remplaçant n par n+1 ds l'expression que l'on doit démontrer ainsi P(n+1) est vrais ossi or comme P1 est vraie Pn est vraie pour tt n sup ou égal à 1 et : 1+4+8+...+n^2 = [n(n+1)(2n+1)]/6.

[Quidam]

Bonjour,

On considére n sphère concentriques de centre O et de rayon respectifs 1,2,3,...,n,n+1.

Euh, moi j'en vois (n+1) (des sphères) et pas seulement n, mais bon !

1) Déterminer le volume V de la plus grosse sphère ( ou boule) extérieur.

On suppose connue la formule donnant le volume d'une sphère de rayon R :
Donc le volume de la plus grande sphère est :

2)On appelle Vk le volume délimité par les sphères de rayon k et de rayon k+1.

a) Montrer que Vk= 4/3 pi (3k² + 3k + 1).

2)a)

b) Exprimer V en fonction de Vk.

2)b)
V est le volume de la sphère de rayon (n+1) ; il est clair que c'est la somme du volume de la plus petite sphère et du volume entre la sphère de rayon 1 et celle de rayon 2 (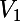) et du volume entre la sphère de rayon 2 et celle de rayon 3 () et ainsi de suite, jusqu'au volume entre la sphère de rayon n et celle de rayon (n+1) (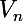). Par conséquent :

[quote="ayana77"]
3) En déduire que (n+1) au cube =3(1²+2²+3²+...+n²) + 3(1+2+3+...+n) +n+1



Nous avons montré précédemment que
Donc :


Sauras-tu terminer ?

[thomasgogo]

Salut quidam je sais que cela fait un bail que ce sujet n'est pas relancer et je demande ton aide car j'ai le même devoir en maths pourrais-tu m'aider pour les question 3 et 4 ? Merci d'avance

[ninouchou]

Salut,
J'ai vraiment besoin d'aide pour la question 4, Thomasgogo, peut être as tu eu la correction ?
Toute aide serait la bienvenue ;)
merci d'avance

[thomasgogo]

Désolé je n'ai pas eu encore la correction, je pense avoir reussi le reste mais dans le doute, j'attendrai la correction pour ne pas faire d'erreurs. Je pense l'avoir lundi 11 novembre .