Suite récurrente linéaire d'ordre 4
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 01 Jan 2009, 14:56
par Zweig » 01 Jan 2009, 14:56
Bonjour,
Un exercice sympa pour commencer l'année 2009 en forme ! :zen:
Soit
)
la suite définie par
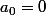
,
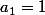
,
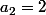
,
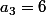
et :
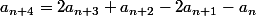
Montrer que pour tout
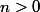
,

est un multiple de

-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 01 Jan 2009, 15:10
par ThSQ » 01 Jan 2009, 15:10
C'est n*fibonacci, marrant
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 01 Jan 2009, 15:14
par Zweig » 01 Jan 2009, 15:14
Exact :zen:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 01 Jan 2009, 15:20
par lapras » 01 Jan 2009, 15:20
Récurrence :
U_n = F_n*n
F_n : suite de fibonaci
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 01 Jan 2009, 15:22
par Zweig » 01 Jan 2009, 15:22
Oui bon, ça c'est le plus facile à voir, après faut dérouler la récurrence (même si elle n'est pas si insurmontable que ça).
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 01 Jan 2009, 15:27
par lapras » 01 Jan 2009, 15:27
Je l'ai faite : quelques lignes de calculs et tout est juste. (l'idée est de réduire tout en F_{n+1} et F_n)
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 01 Jan 2009, 17:50
par ThSQ » 01 Jan 2009, 17:50
Enfin à mon avis c'est plus simple de montre que n*Fn vérifie la même équation (et comme les deux suites démarrent de la même façon ...).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités