Suite récurrente linéaire d'ordre 3 - Carré parfait
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 09 Oct 2008, 20:37
par Zweig » 09 Oct 2008, 20:37
Salut,
Un 'tit exo sympa :
Soit
)
une suite définie par récurrence :
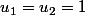
,
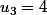
et
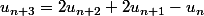
Montrer que pour tout entier naturel

,

est un carré.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Oct 2008, 02:57
par Doraki » 10 Oct 2008, 02:57
Soit
)
une suite vérifiant la relation
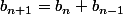
Alors la suite
 = (b_n^2))
vérifie la relation
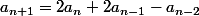
:
Preuve simple : (B + (A+B))² = (A+2B)² = A² + 4AB + 4B² = 2(A+B)² + 2B² - A²
Dans notre cas, on a
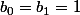
et
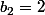
donc
)
vérifie bien ce qu'il faut.
Et bien sûr,
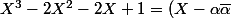(X - \alpha^2)(X - \bar\alpha^2))
où

et
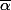
sont les racines de X²-X-1.
J'imagine que ça se généralise assez bien pour le produit de plusieurs suites avec des relations de récurrences quelconques, en faisant gaffe aux multiplicités des racines.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 10 Oct 2008, 17:17
par Zweig » 10 Oct 2008, 17:17
Oui, c'est ça ! Enfin, c'est plus "visible" si on remarque (ce qu'il faut prouver) que
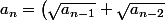^{2})
(qui "ressemble" à la suite de Fibonacci), car ta suite
)
, aux premiers abords, on ne voit pas trop d'où elle vient. :id:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités