Nombres premiers et carré parfait
Olympiades mathématiques, énigmes et défis
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 20 Fév 2007, 14:13
par BiZi » 20 Fév 2007, 14:13
Bonjour,
Soient n > 1 un entier et p un nombre premier tel que n divise p-1 et p divise n^3 - 1. Prouver que 4p-3 est un carré.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 20 Fév 2007, 18:00
par aviateurpilot » 20 Fév 2007, 18:00
merci pour l'exo
Bizi,
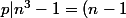(n^2+n+1))
et

si

alors

et on a

donc

absurde
donc

(car

premier).
par suite,
\in{\mathbb{N}}^*;\ tel\ que\ n^2+n+1=sp\ et\ p=kn+1)

=>
=s-1)
=>

donc si

,alors

=>
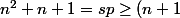(n+1))
absurde
donc
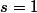
et on aura
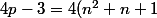-3=(2n+1)^2)
qui un carré parfait.
un autre exo stp et merci d'avance. :++:
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 20 Fév 2007, 18:49
par BiZi » 20 Fév 2007, 18:49
Bon, en voici un autre dans la foulée, tiré d'un dossier du tutorat toujours:
Soit p un nombre premier congru à 2 modulo 3. Soient a et b deux entiers tels que p divise a^2 + ab + b^2. Prouver que p divise a et b.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 20 Fév 2007, 19:50
par aviateurpilot » 20 Fév 2007, 19:50
le probleme est à:
(*) a écrit:si

alors l'application
=x^3)
est injective.
autrement dit
^3} \}=p)
(*)
je vais essayer de montrer
)
et par la suite j'aurai le droit d'ecrire

=>
\equiv f(b)[p])
=>

=>

=>

et par la suite

-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 21 Fév 2007, 11:51
par aviateurpilot » 21 Fév 2007, 11:51
supposant que
\in (\mathbb{N}-p\mathbb{N})^2)


=>

=>
^3\equiv (ua)^3[p]\equiv 1[p])
=>
^{p-2}\equiv ((ub)^3)^{\frac{p-2}{3}}[p]\equiv 1[p])
=>
^{p-1}\equiv ub[p])
=>

=>

=>

=>
 absurde.
absurde.donc
\in (p\mathbb{N})^2)
un autre exo i c'est possible lol
:++:
-
musichien
- Membre Naturel
- Messages: 35
- Enregistré le: 02 Aoû 2006, 15:45
-
 par musichien » 26 Fév 2007, 19:00
par musichien » 26 Fév 2007, 19:00
De tête, le dernier exo de ce fameux dossier:
Soit
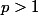
un entier fixé.
_{i\geq 0})
est une suite de naturels périodique dès le début.
Montrer qu'il existe des suite d'entiers,
)
et
)
, telles que

et

pour tout

,
)
étant périodique.
ça devrait t'occuper un peu. :happy2:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 01 Mar 2007, 17:46
par aviateurpilot » 01 Mar 2007, 17:46
musichien a écrit:De tête, le dernier exo de ce fameux dossier:
Soit
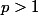
un entier fixé.
_{i\geq 0})
est une suite de naturels périodique dès le début.
Montrer qu'il existe des suite d'entiers,
)
et
)
, telles que

et

pour tout

,
)
étant périodique.
ça devrait t'occuper un peu. :happy2:
on prend tout simplement

musichien a écrit:ça devrait t'occuper un peu. :happy2:
hhhh. je viens de voir ton exo, je ne pense pas que c'est un exo olympiades.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
un entier fixé.
est une suite de naturels périodique dès le début.
et
, telles que
et
pour tout
,
étant périodique.
