Suite d’entiers

[MMu]

Montrer que la suite ( entier > 0) contient une infinité de termes de la forme ( entier > 0)

[Ben314]

Salut,
Soit je me goure, soit c'est assez simple :
Pour un donné, le seul susceptible de vérifier est et il marche ssi la partie fractionnaire de est strictement supérieure à .
Si tel est le cas, c'est gagné, et sinon, vu que on a qui marche si , sinon , etc . . . Et ça fini forcément par marcher vu que est irrationnel donc est non nul.

[MMu]

La démarche de Ben est très différente de la mienne , et je suis très intéressé de la voir marcher. Pour l’instant je ne suis pas convaincu...

[catamat]

J'ai vérifié la solution de Ben314, tout est nickel.

J'obtiens le tableau suivant :

[Ben314]

Moi, ça me semble aussi O.K., mais la méthode ne marche que parce que la "barre" .
Alors que j'aurais tendance à penser que, si on part d'un irrationnel (ici ) et d'un entier (ici 3), alors la suite des parties fractionnaire des est dense dans [0,1] (ce qui signifierais que, même si la "barre" était bien plus grande, il y aurait quand même une infinité de pour lesquels ça marche)
J'ai pas vraiment cherché à voir si c'était vrai et facilement démontrable.

[MMu]

C’est assez facilement démontrable.....
Voir un problème voisin déjà vu ici il y a quelques jours

[catamat]

Pour moi je le vois ainsi : (solution de Ben314 détaillée)
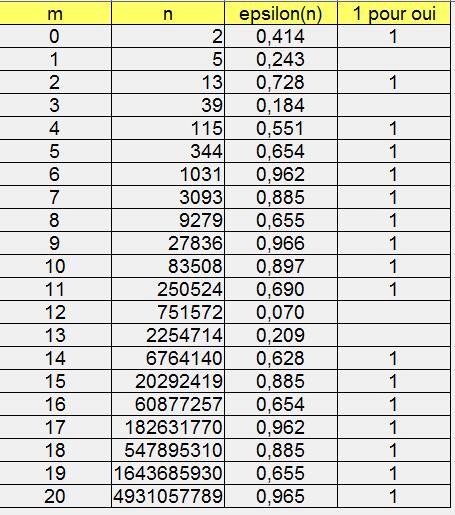
Soit m un entier, on pose
où est la partie entière et la partie décimale.

On a car est irrationnel.

On cherche un entier n tel que

donc en divisant par la racine carrée de 2 et en utilisant les notations précédentes :

Dans cet intervalle il n'y a qu'un seul entier c'est
Mais si et seulement si (d'après l'inégalité précédente)

ou

Bon la suite Ben314 l'a explicitée... en gros si ça marche pas pour un certain m, cela marchera pour le suivant ou celui d'après etc..

[MMu]

[quote="Ben314"]Moi, ça me semble aussi O.K., mais la méthode ne marche que parce que la "barre" .
Alors que j'aurais tendance à penser que, si on part d'un irrationnel (ici ) et d'un entier (ici 3), alors la suite des parties fractionnaire des est dense dans [0,1] (ce qui signifierais que, même si la "barre" était bien plus grande, il y aurait quand même une infinité de pour lesquels ça marche)
J'ai pas vraiment cherché à voir si c'était vrai et facilement démontrable.[\quote]

Comme d’habitude Ben314 a le talent de soulever une question intéressante (concernant la "densité")
Je pense qu’en général ce n’est pas vrai .
Par ex considérons la représentation en base 2 : avec 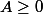entier et
Construisons maintenant en base 3 :
Évidemment pour les parties fractionnaires on a et évidemment leur ensemble n’est pas dense dans ...

[Ben314]

Effectivement, ma conjecture est franchement fausse et ça se voit bien avec l'écriture de en base .
Et si on suppose par exemple que est quadratique, peut-on dire quelque chose ?