Indépendance et proba nulle
64 messages
- Page 2 sur 4 - 1, 2, 3, 4
Re: Probas: accorder ou non l'indépendance!
[quote=".................................................
Modifié en dernier par beagle le 18 Mai 2019, 13:30, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probas: accorder ou non l'indépendance!
Bonjour
Je réponds en particulier à @pseuda:
Pour faire des calculs, il faut bien modéliser c'est à dire passer à l'abstrait en établissant des règles bien précises.
Une fois que l'on a admis ce qu'est une variable aléatoire à densité et deux évènement indépendants
il ne faut pas s'étonner d'obtenir les deux exemples cités précédemment même si cela peut choquer l'intuition.
Si je prends l'exemple d'une flèche qui se plante en un point précis de coordonnées polaires par exemple
) c'est à dire à distance
c'est à dire à distance  du centre qu'est ce que cela peut dire?
du centre qu'est ce que cela peut dire?
La pointe de la flèche n'étant pas de dimension infinitésimale. Mais on a modélisé et je ne vois pas pourquoi on va l'oublier.
Pour un nombre tiré au hasard dans [0,1] c'est la même chose.
Je réponds en particulier à @pseuda:
Pour faire des calculs, il faut bien modéliser c'est à dire passer à l'abstrait en établissant des règles bien précises.
Une fois que l'on a admis ce qu'est une variable aléatoire à densité et deux évènement indépendants
il ne faut pas s'étonner d'obtenir les deux exemples cités précédemment même si cela peut choquer l'intuition.
Si je prends l'exemple d'une flèche qui se plante en un point précis de coordonnées polaires par exemple
La pointe de la flèche n'étant pas de dimension infinitésimale. Mais on a modélisé et je ne vois pas pourquoi on va l'oublier.
Pour un nombre tiré au hasard dans [0,1] c'est la même chose.
Re: Probas: accorder ou non l'indépendance!
Si la flèche se plante à 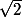 , on ne peut pas le savoir. Il faudrait aller mesurer, et on n'en serait jamais sûr, il faudrait ajouter des décimales, la probabilité tendrait vers 1, mais ne serait pas 1.
, on ne peut pas le savoir. Il faudrait aller mesurer, et on n'en serait jamais sûr, il faudrait ajouter des décimales, la probabilité tendrait vers 1, mais ne serait pas 1.
De toute façon, il est impossible que la flèche se plante précisément à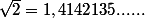 , avec des points qui ne s'arrêtent jamais. Et si on demande à quelqu'un de penser à nombre compris entre 1 et 2, et qu'il pense précisément à
, avec des points qui ne s'arrêtent jamais. Et si on demande à quelqu'un de penser à nombre compris entre 1 et 2, et qu'il pense précisément à 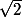 , ce n'est pas le fruit du hasard complet, car
, ce n'est pas le fruit du hasard complet, car 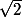 est nombre connu, répertorié : le fruit d'un nombre tiré au hasard serait impossible à penser (à l'avance ou non, cela ne change rien).
est nombre connu, répertorié : le fruit d'un nombre tiré au hasard serait impossible à penser (à l'avance ou non, cela ne change rien).
De toute façon, il est impossible que la flèche se plante précisément à
Re: Probas: accorder ou non l'indépendance!
[.........................................
Modifié en dernier par beagle le 18 Mai 2019, 13:33, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probas: accorder ou non l'indépendance!
@beagle On ne peut pas parler de P(A sachant A) si P(A)=0.
P(A sachant B) est la probabilité que A se réalise sachant que B s'est réalisé, autrement dit dans l'univers où B est réalisé, mais si P(B)=0, ceci est impossible.
@aviateur Je reviens à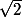 . On peut le voir aussi en disant que si la flèche avait la moindre chance de tomber sur
. On peut le voir aussi en disant que si la flèche avait la moindre chance de tomber sur 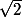 , et en supposant (évidemment) que les probabilités de tomber sur n'importe quel nombre compris entre 1 et 2 sont les mêmes, alors la somme des probabilités serait infinie. Donc par contraposée... (vous l'aurez compris, je déteste les paradoxes, et cherche toujours à trouver une explication rationnelle).
, et en supposant (évidemment) que les probabilités de tomber sur n'importe quel nombre compris entre 1 et 2 sont les mêmes, alors la somme des probabilités serait infinie. Donc par contraposée... (vous l'aurez compris, je déteste les paradoxes, et cherche toujours à trouver une explication rationnelle).
Paradoxalement, on réfute les démonstrations basées sur les probabilités. Si une assertion a une probabilité certaine d'être vraie, on ne la tient pas pour autant démontrée :
enigmes/conjecture-goldbach-elucidation-par-analyse-structurelle-t185643.html?hilit=conjjecture%20de%20goldbach#p1232067
P(A sachant B) est la probabilité que A se réalise sachant que B s'est réalisé, autrement dit dans l'univers où B est réalisé, mais si P(B)=0, ceci est impossible.
@aviateur Je reviens à
Paradoxalement, on réfute les démonstrations basées sur les probabilités. Si une assertion a une probabilité certaine d'être vraie, on ne la tient pas pour autant démontrée :
enigmes/conjecture-goldbach-elucidation-par-analyse-structurelle-t185643.html?hilit=conjjecture%20de%20goldbach#p1232067
Re: Probas: accorder ou non l'indépendance!
"beagle On ne peut pas parler de P(A sachant A) si P(A)=0.
P(A sachant B) est la probabilité que A se réalise sachant que B s'est réalisé, autrement dit dans l'univers où B est réalisé, mais si P(B)=0, ceci est impossible."
Perso j'y arrive très bien. A éviter pour Skullkid, attention au troll:
Proba que la flèche soit en A sachant qu'elle est tombée en A, ben c'est 1.
Proba que la flèche soit en A sacahnt qu'elle est tombée en B, ben c'est 0
Et ceci car il ya deux zéros.
Le zéro de 1/infini et le zero du qu'existe pas de l'ensemble vide
prenons la flèche tombe en A de proba = 0
la flèche tombe en B de proba = 0
proba de A sachant A c'est 0/0
avec 0 est 1/infini de la proba A inter A qui est A
et en dessous 0 de 1/infini proba de a
ce 0/0 est le 1
proba de A sachant B est 0/0
avec le zéro qui vaut un vrai zéro de A inter B
et en dessous le zero de 1:infini du p de B
0 / 1/infini
qui donne zero
p A sachant B = 0
Voilà c'est cohérent.
P(A sachant B) est la probabilité que A se réalise sachant que B s'est réalisé, autrement dit dans l'univers où B est réalisé, mais si P(B)=0, ceci est impossible."
Perso j'y arrive très bien. A éviter pour Skullkid, attention au troll:
Proba que la flèche soit en A sachant qu'elle est tombée en A, ben c'est 1.
Proba que la flèche soit en A sacahnt qu'elle est tombée en B, ben c'est 0
Et ceci car il ya deux zéros.
Le zéro de 1/infini et le zero du qu'existe pas de l'ensemble vide
prenons la flèche tombe en A de proba = 0
la flèche tombe en B de proba = 0
proba de A sachant A c'est 0/0
avec 0 est 1/infini de la proba A inter A qui est A
et en dessous 0 de 1/infini proba de a
ce 0/0 est le 1
proba de A sachant B est 0/0
avec le zéro qui vaut un vrai zéro de A inter B
et en dessous le zero de 1:infini du p de B
0 / 1/infini
qui donne zero
p A sachant B = 0
Voilà c'est cohérent.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probas: accorder ou non l'indépendance!
Sinon Pseuda tu argumentes sur la précision,
mais es-tu contre le fait qu'un évènement de proba égale zéro soit possible?
mais es-tu contre le fait qu'un évènement de proba égale zéro soit possible?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probas: accorder ou non l'indépendance!
J'ai exactement la même opinion que Pseuda : un événement de proba nulle, dans le concret, ça veut dire qu'il ne peut pas arriver et puis c'est tout.
Et la loi uniforme sur [0,1], quand on l'utilise "dans le concret", c'est pour modéliser un truc où, bien sûr, il n'y a qu'un nombre fini (mais très grand) de résultat possible. Dans la monde concret, l'infini, ça n'existe pas : c'est uniquement une "vue de l'esprit" qu'utilise (depuis pas si longtemps que ça) les matheux pour simplifier les problèmes, par exemple pour pouvoir parler de continuité.
Et évidement, pour la ça cible, c'est exactement la même chose : elle est constituée d'atomes en nombre fini et la pointe de la fléchette ne va pas couper un atome en deux : il n'y a de nouveau et bien évidement qu'un nombre fini d'issues possible et la proba. que la fléchette tape à un endroit donné n'est pas nulle, elle est seulement très faible.
Bref, il faut remettre les pieds sur terre : toute modélisation mathématique faisant appel à l'infini est forcément et par nature même une "vue de l'esprit" et, comme tout ce touche à l'infini, ben il faut évidement se méfier comme la peste de toute interprétation hâtive (i.e. sans réfléchir au fait que ce n'est évidement qu'une vue de l'esprit simplificatrice et sûrement pas la réalité)
Et la loi uniforme sur [0,1], quand on l'utilise "dans le concret", c'est pour modéliser un truc où, bien sûr, il n'y a qu'un nombre fini (mais très grand) de résultat possible. Dans la monde concret, l'infini, ça n'existe pas : c'est uniquement une "vue de l'esprit" qu'utilise (depuis pas si longtemps que ça) les matheux pour simplifier les problèmes, par exemple pour pouvoir parler de continuité.
Et évidement, pour la ça cible, c'est exactement la même chose : elle est constituée d'atomes en nombre fini et la pointe de la fléchette ne va pas couper un atome en deux : il n'y a de nouveau et bien évidement qu'un nombre fini d'issues possible et la proba. que la fléchette tape à un endroit donné n'est pas nulle, elle est seulement très faible.
Bref, il faut remettre les pieds sur terre : toute modélisation mathématique faisant appel à l'infini est forcément et par nature même une "vue de l'esprit" et, comme tout ce touche à l'infini, ben il faut évidement se méfier comme la peste de toute interprétation hâtive (i.e. sans réfléchir au fait que ce n'est évidement qu'une vue de l'esprit simplificatrice et sûrement pas la réalité)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Probas: accorder ou non l'indépendance!
Salut Ben314
"J'ai exactement la même opinion que Pseuda : un événement de proba nulle, dans le concret, ça veut dire qu'il ne peut pas arriver et puis c'est tout."
cela change beaucoup de choses,
je croyais que c'était sérieux j'ai lu sur ce site même un évènement de proba nulle qui était possible et je l'ai lu sur le web de pages qui paraissaient sérieuses.
Je confonds avec une autre notion ou quoi?
Tu peux nous en dire plus sur ce truc.
parce que moi depuis le début je me dépatouille avec cette notion que il existe des évènements de proba nulle qui peuvent survenir.
Pour la flèche ben c'est théorique il s'agit d'atterrir en étant centré alors sur un point de dimension zero., non?
"J'ai exactement la même opinion que Pseuda : un événement de proba nulle, dans le concret, ça veut dire qu'il ne peut pas arriver et puis c'est tout."
cela change beaucoup de choses,
je croyais que c'était sérieux j'ai lu sur ce site même un évènement de proba nulle qui était possible et je l'ai lu sur le web de pages qui paraissaient sérieuses.
Je confonds avec une autre notion ou quoi?
Tu peux nous en dire plus sur ce truc.
parce que moi depuis le début je me dépatouille avec cette notion que il existe des évènements de proba nulle qui peuvent survenir.
Pour la flèche ben c'est théorique il s'agit d'atterrir en étant centré alors sur un point de dimension zero., non?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probas: accorder ou non l'indépendance!
J'ai retrouvé:
http://images.math.cnrs.fr/Le-negligeab ... pas-l.html
Et sur le site maths forum j'avais lu une telle notion de la part de Nightmare, doraki sans doute était là, tu n'y étais pas Ben314?
http://images.math.cnrs.fr/Le-negligeab ... pas-l.html
Et sur le site maths forum j'avais lu une telle notion de la part de Nightmare, doraki sans doute était là, tu n'y étais pas Ben314?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probas: accorder ou non l'indépendance!
J'ai l'impression de me répéter, mais dans le monde des mathématiques, (donc une vue de l'esprit) c'est effectivement on ne peut plus possible vu qu'il y a des tas de trucs infinis, par exemple le nombre de points sur le segment [0,1], mais c'est bien évidement faux dans le monde réel : quoi que tu mesure, découpe, partitionne dans le monde réel il y a un moment ou tu ne peut pas aller plus loin donc il n'y a que et exclusivement que des "probas discrètes". Sauf que bien évidement, si le nombre de cas est grand, la meilleure façon de voir le bidule sur le plan mathématique, c'est de faire comm s'il y avait une infinité d'issue possible.
Mais quand tu modélise un problème concret à l'aide d'une loi continue, par exemple une répartition uniforme sur [0,1], il faut bien comprendre que des trucs du style p(X=a)=0, c'est du "pur abstrait" vu que ça n'a pas le moindre sens concret de parler d'une valeur exacte de X, on n'a évidement que des approximation donc seule les proba du style p(X entre a et b) ont du sens concrètement parlant.
Bref, concrètement parlant, ça veut rien dire de se demander si pour une loi uniforme l’événement "X=a" est indépendant ou pas de je sais pas quel autre événement.
Mais quand tu modélise un problème concret à l'aide d'une loi continue, par exemple une répartition uniforme sur [0,1], il faut bien comprendre que des trucs du style p(X=a)=0, c'est du "pur abstrait" vu que ça n'a pas le moindre sens concret de parler d'une valeur exacte de X, on n'a évidement que des approximation donc seule les proba du style p(X entre a et b) ont du sens concrètement parlant.
Bref, concrètement parlant, ça veut rien dire de se demander si pour une loi uniforme l’événement "X=a" est indépendant ou pas de je sais pas quel autre événement.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Probas: accorder ou non l'indépendance!
Je suis allé jeter un coup d’œil sur l'article et je trouve pas son argumentaire pertinent du tout en ce qui concerne la deuxième objection.
Le type qui répond parle ensuite des négligeables de façon générale dans la théorie de Lebesgue, mais je voudrait bien savoir ce qu'ils en pense du fait que dans la théorie en question, il existe non seulement des ensemble négligeable (par exemple un point isolé), mais il existe aussi des ensemble non mesurable, c'est à dire qu'il existe des "zones" sur la cible où ça n'a pas de sens (y compris de sens mathématique) de demander quelle est la proba. que la fléchette tombe dans cette zone là.
Ça te semble "concret" ça que certaines parties de la cible n'ont pas de proba associée ?
Le type qui répond parle ensuite des négligeables de façon générale dans la théorie de Lebesgue, mais je voudrait bien savoir ce qu'ils en pense du fait que dans la théorie en question, il existe non seulement des ensemble négligeable (par exemple un point isolé), mais il existe aussi des ensemble non mesurable, c'est à dire qu'il existe des "zones" sur la cible où ça n'a pas de sens (y compris de sens mathématique) de demander quelle est la proba. que la fléchette tombe dans cette zone là.
Ça te semble "concret" ça que certaines parties de la cible n'ont pas de proba associée ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Probas: accorder ou non l'indépendance!
ah .............................................
Modifié en dernier par beagle le 18 Mai 2019, 13:29, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probas: accorder ou non l'indépendance!
autres refs:
https://books.google.fr/books?id=rprNjz ... le&f=false
autre vision, le zero des mathématiciens et le zero des probabileux. :
http://artandscienceprojects.be/wp-cont ... %C3%A9.pdf
mais différent de notre problème initial je pense
mais qui peut expliquer l'usage que ...
https://books.google.fr/books?id=rprNjz ... le&f=false
autre vision, le zero des mathématiciens et le zero des probabileux. :
http://artandscienceprojects.be/wp-cont ... %C3%A9.pdf
mais différent de notre problème initial je pense
mais qui peut expliquer l'usage que ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probas: accorder ou non l'indépendance!
Donc le troll va continuer.
Ceux qui comme Pseuda et Ben314 disent proba nulle c'est évènement impossible,
alors je comprends qu'ils gardent la formule de l'indépendance telle que.
au niveau cohérence je ne fais pas de relance.
Pour ceux qui acceptent les évènements de proba nulle comme pouvant se realiser,
que faites vous de la notion d'indépendance, gardez vous la formule générale,
continuez vous à dire que A est indépendant de A,
dites-vous que si A est réalisé alors la proba que cela soit A est nulle…
a vos plumes!
Ceux qui comme Pseuda et Ben314 disent proba nulle c'est évènement impossible,
alors je comprends qu'ils gardent la formule de l'indépendance telle que.
au niveau cohérence je ne fais pas de relance.
Pour ceux qui acceptent les évènements de proba nulle comme pouvant se realiser,
que faites vous de la notion d'indépendance, gardez vous la formule générale,
continuez vous à dire que A est indépendant de A,
dites-vous que si A est réalisé alors la proba que cela soit A est nulle…
a vos plumes!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probas: accorder ou non l'indépendance!
Bonjour,
Pour résumer, la flèche n'avait aucune chance de tomber sur . Si elle y est tombée, c'est que :
. Si elle y est tombée, c'est que :
- soit il y a un biais dans l'expérience aléatoire : la probabilité n'est pas aussi uniforme qu'elle en a l'air ( est un nombre répertorié, connu, qui n'a pas été choisi complétement au hasard) ; ce cas est compris dans le cas suivant :
est un nombre répertorié, connu, qui n'a pas été choisi complétement au hasard) ; ce cas est compris dans le cas suivant :
- soit la probabilité n'est pas si continue qu'elle en a l'air (argument de Ben314 : la continuité n'existe pas dans la vie réelle, et ici il s'agit d'une telle expérience : la pointe de la flèche n'est pas si aiguisée qu'on pourrait le croire, ou les points de la cible ne sont pas de dimension nulle).
Mais si on fait l'expérience suivante : on demande à deux personnes, l'une de penser à un nombre compris entre 0 et 1, l'autre de le deviner. Pour que l'expérience soit sans biais, la 1ère personne récite les décimales les unes après les autres et les écrit sur un papier caché de la 2ème personne, la 2ème personne les devine. Le jeu s'arrête quand la 2ème personne se trompe. Eh bien, la probabilité que le jeu ne s'arrête pas (c-a-d que le nombre trouvé est exactement celui choisi) est nulle.
Par contre, je ne dirais pas que la continuité n'existe pas dans la vie réelle (pour moi, elle existe dans un certain contexte jusqu'à preuve du contraire : les points d'un segment, les nombres entre 0 et 1, les couleurs de l'arc en ciel, l'écoulement du temps, sont, ou nous paraissent, étagés continûment), je dirais qu'elle est difficile à reproduire concrètement (comme dans l'expérience de la flèche, ou du jeu à 2 personnes). Jusqu'à une période récente, on pensait que le temps s'écoulait continûment. Les derniers développements de la physique nous disent que c'est faux (le temps s'écoule par très petits sauts). Mais qui nous dit que des développements ultérieurs ne vont pas conclure à l'inverse (puisqu'on s'est déjà trompés une fois, on ne peut pas exclure qu'on se trompe une 2ème fois). Il ne faut rien exclure, nos conclusions sont celles à l'instant présent.
Pour résumer, la flèche n'avait aucune chance de tomber sur
- soit il y a un biais dans l'expérience aléatoire : la probabilité n'est pas aussi uniforme qu'elle en a l'air (
- soit la probabilité n'est pas si continue qu'elle en a l'air (argument de Ben314 : la continuité n'existe pas dans la vie réelle, et ici il s'agit d'une telle expérience : la pointe de la flèche n'est pas si aiguisée qu'on pourrait le croire, ou les points de la cible ne sont pas de dimension nulle).
Mais si on fait l'expérience suivante : on demande à deux personnes, l'une de penser à un nombre compris entre 0 et 1, l'autre de le deviner. Pour que l'expérience soit sans biais, la 1ère personne récite les décimales les unes après les autres et les écrit sur un papier caché de la 2ème personne, la 2ème personne les devine. Le jeu s'arrête quand la 2ème personne se trompe. Eh bien, la probabilité que le jeu ne s'arrête pas (c-a-d que le nombre trouvé est exactement celui choisi) est nulle.
Par contre, je ne dirais pas que la continuité n'existe pas dans la vie réelle (pour moi, elle existe dans un certain contexte jusqu'à preuve du contraire : les points d'un segment, les nombres entre 0 et 1, les couleurs de l'arc en ciel, l'écoulement du temps, sont, ou nous paraissent, étagés continûment), je dirais qu'elle est difficile à reproduire concrètement (comme dans l'expérience de la flèche, ou du jeu à 2 personnes). Jusqu'à une période récente, on pensait que le temps s'écoulait continûment. Les derniers développements de la physique nous disent que c'est faux (le temps s'écoule par très petits sauts). Mais qui nous dit que des développements ultérieurs ne vont pas conclure à l'inverse (puisqu'on s'est déjà trompés une fois, on ne peut pas exclure qu'on se trompe une 2ème fois). Il ne faut rien exclure, nos conclusions sont celles à l'instant présent.
Re: Probas: accorder ou non l'indépendance!
Je vais reprendre ce point sur un fil dédié si j'ai le temps,
car cela ne passe pas.
Je n'ai pas besoin de connaitre le nombre dans l'expérience de la flèche, ce n'est pas un nombre, c'est un lieu,
et si on approxime l'entrée de la flèche à un cercle, si on dit que ce qui est observé est le centre du cercle.
Alors on parle de la probabilité d'un point.
Que je ne puisse avoir ses coordonnées exactes ne change rien au fait que la flèche est tombée sur ce point.
Ce point de dimension zéro nous sommes d'accord, donc inutile de parler d'atomes et physique, le point n'est pas matériel, c'est un lieu donné.
Et ce point avait une probabilité zéro d'ètre atteint par la flèche = d'ètre le centre du cercle d'entrée de la pointe.
Je ne vois aucune raison de faire de la physique, on fait de la géométrie de ce genre sans se poser de question.
car cela ne passe pas.
Je n'ai pas besoin de connaitre le nombre dans l'expérience de la flèche, ce n'est pas un nombre, c'est un lieu,
et si on approxime l'entrée de la flèche à un cercle, si on dit que ce qui est observé est le centre du cercle.
Alors on parle de la probabilité d'un point.
Que je ne puisse avoir ses coordonnées exactes ne change rien au fait que la flèche est tombée sur ce point.
Ce point de dimension zéro nous sommes d'accord, donc inutile de parler d'atomes et physique, le point n'est pas matériel, c'est un lieu donné.
Et ce point avait une probabilité zéro d'ètre atteint par la flèche = d'ètre le centre du cercle d'entrée de la pointe.
Je ne vois aucune raison de faire de la physique, on fait de la géométrie de ce genre sans se poser de question.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probas: accorder ou non l'indépendance!
......................................................
Modifié en dernier par beagle le 18 Mai 2019, 13:28, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probas: accorder ou non l'indépendance!
@ Beagle :
Ce n'est pas parce que la flèche tombe sur un point que pour autant la proba qu'elle avait de tomber sur un point précis désigné auparavant n'est pas nulle. La proba, c'est le ratio entre l'événement attendu et le nombre d'événements possibles. Ici, dans ton cas, la proba de tomber sur un point désigné à l'avance est nulle, car elle est de 1 / infini = 0 en supposant tous les points équiprobables.
Je ne vois pas en quoi c'est contradictoire.
Ce n'est pas parce que la flèche tombe sur un point que pour autant la proba qu'elle avait de tomber sur un point précis désigné auparavant n'est pas nulle. La proba, c'est le ratio entre l'événement attendu et le nombre d'événements possibles. Ici, dans ton cas, la proba de tomber sur un point désigné à l'avance est nulle, car elle est de 1 / infini = 0 en supposant tous les points équiprobables.
Je ne vois pas en quoi c'est contradictoire.
Re: Probas: accorder ou non l'indépendance!
" .................................................
.
.
Modifié en dernier par beagle le 18 Mai 2019, 13:29, modifié 4 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
64 messages
- Page 2 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
