Petit défi de proba
24 messages
- Page 1 sur 2 - 1, 2
Petit défi de proba
Hello à tous,
Dans la tradition des défis, j'en pose un assez sympa et dont le résultat m'a personnellement impressionné.
On se donne deux jeux identiques de n cartes à jouer, qu'on retourne face cachée.
Pour commencer, on retourne ensemble les deux premières cartes de chaque paquet, puis les deux suivantes, ... jusqu'à la fin du paquet. Quelle est la probabilité de NE PAS avoir vu deux cartes identiques retournées en même temps lorsque n devient grand ?
C'est assez difficile, mais joli !
Lucas
PS : Le résultat est assez classique donc ceux qui connaissent peuvent donner des indices !
Dans la tradition des défis, j'en pose un assez sympa et dont le résultat m'a personnellement impressionné.
On se donne deux jeux identiques de n cartes à jouer, qu'on retourne face cachée.
Pour commencer, on retourne ensemble les deux premières cartes de chaque paquet, puis les deux suivantes, ... jusqu'à la fin du paquet. Quelle est la probabilité de NE PAS avoir vu deux cartes identiques retournées en même temps lorsque n devient grand ?
C'est assez difficile, mais joli !
Lucas
PS : Le résultat est assez classique donc ceux qui connaissent peuvent donner des indices !
Darkwolftech a écrit:C'est ça :lol3:
ça doit donner 1/n, non ?
(blank)
Je pars du principe que dans un jeu, toutes les cartes sont différentes
On peur alors considérer un jeu de carte comme une permutation de E = {1 ; ... ; n }.
On cherche donc la probabilité que deux éléments f1 et f2 de perm(E) n'aient aucune valeur en commun : pour tout x de E, f1(x) est différent de f2(x).
On peut, sans perte de généralité, considérer que f1 est l'identité.
On sait déjà que le cardinal de Perm(E) est n!
On cherche donc le cardinal du l'ensemble de Perm(E) vérifiant :
{ f appartient à perm(E) et pour tout x de E, f(x) x }
A priori (j'ai la flemme de détailler), il n'y en a "que" (n-1)!
La probabilité cherchée est donc (n-1)!/n! = 1/n
C'est quoi exactement ta généralisation de l'énoncé du problème avec k paquets.Matt_01 a écrit:...(Pour k paquets j'ai un équivalent en l'infini).
Tu veut que les k cartes retournées sur les k paquets soient toutes les mêmes ou bien qu'il y en ait au moins deux d'identique ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Matt_01 a écrit:Le raisonnement est là mais le dénombrement annoncé est faux.
(Pour k paquets j'ai un équivalent en l'infini).
Si on représente une permutation par des pions sur un damier de taille n x n (il doit y avoir un pion par ligne et un par colonne), cela reviens à interdire la diagonale aux pions.
C'est pas évident, il faudrait que je cherche plus longtemps. En fait tout la difficulté est là.
Ben314 a écrit:C'est quoi exactement ta généralisation de l'énoncé du problème avec k paquets.
Tu veut que les k cartes retournées sur les k paquets soient toutes les mêmes ou bien qu'il y en ait au moins deux d'identique ?
Au moins 2 d'identiques. J'avais même pas pensé à l'autre cas de figure, à voir.
Déjà, pour k=3, ça donne ça (à diviser par (n!)² pour avoir la proba de ne jamais avoir 2 cartes identiques)
https://oeis.org/A000186
Et on peut pas dire que ça se simplifie des tonnes...
https://oeis.org/A000186
Et on peut pas dire que ça se simplifie des tonnes...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Si tu obtient un truc du style "dn fois quelque chose", je suis à peu prés sûr que c'est faux vu que, lorsque tu prend un dérangement f donné (i.e. f(n)n pour tout n), le nombre de permutation g telle que g(n)n et g(n)f(n) va dépendre de la permutation f choisie.Matt_01 a écrit:Si on notele nombre de dérangements et
, j'avais un résultat du type
(à diviser donc par (n!)²). Je suis pas très motivé pour vérifier si ca donne le même résultat que toi Ben, à voir.
Par exemple, pour n=4, les dérangements sont :
- Les 4-cycles (il y en a 6) et, si f est un 4-cyles, il y a 2 fonctions g telles que g(n)n et g(n)f(n) pour tout n.
- Les doubles 2-cycles (il y en a 3) et, si f est un double 2-cyles, il y a 4 fonctions g telles que, pour tout n, g(n)n et g(n)f(n) pour tout n.
Donc au total, il y a 9 dérangement et 6x2+3x4=24 couples (f,g) tels que n,f(n),g(n) soit différents pour tout n.
Or 9 ne divise pas 24.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Sinon, je pense que ton résultat asymptotique, c'était que, lorsqu'il y a k tas (fixé) et que n tend vers l'infini, la proba qu'on ait jamais 2 cartes identiques au sommet des k tas tend vers }{2}\right))
(ce qui fait bien le classique lorsque k=2)
classique lorsque k=2)
(ce qui fait bien le
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Oui.
En fait, j'avais pris pour acquis le fait que pour f un dérangement, E(f)= fDn inter Dn avait un cardinal constant.
Mais quand j'essaye de réfléchir à propos de Dn\E(f)=union sur [|1,n|] des P(f)i ={d dans Dn, d(i)=f-1(i) }, avec la formule du crible on doit calculer le cardinal des dérangements qui partagent k valeurs avec f-1, et je ne vois pas pourquoi c'est différent de)
En fait, j'avais pris pour acquis le fait que pour f un dérangement, E(f)= fDn inter Dn avait un cardinal constant.
Mais quand j'essaye de réfléchir à propos de Dn\E(f)=union sur [|1,n|] des P(f)i ={d dans Dn, d(i)=f-1(i) }, avec la formule du crible on doit calculer le cardinal des dérangements qui partagent k valeurs avec f-1, et je ne vois pas pourquoi c'est différent de
chombier a écrit:ça doit donner 1/n, non ?
(blank)
]Je pars du principe que dans un jeu, toutes les cartes sont différentes
On peur alors considérer un jeu de carte comme une permutation de E = {1 ; ... ; n }.
On cherche donc la probabilité que deux éléments f1 et f2 de perm(E) n'aient aucune valeur en commun : pour tout x de E, f1(x) est différent de f2(x).
On peut, sans perte de généralité, considérer que f1 est l'identité.
On sait déjà que le cardinal de Perm(E) est n!
On cherche donc le cardinal du l'ensemble de Perm(E) vérifiant :
{ f appartient à perm(E) et pour tout x de E, f(x) x }
A priori (j'ai la flemme de détailler), il n'y en a "que" (n-1)!
La probabilité cherchée est donc (n-1)!/n! = 1/n
Ton dénombrement n'est pas bon ...
Petit indice : - Quel est le nombre de permutations laissant un certain i de [| 1,n |] ?
- Puis ensuite, exprime le nombre de permutations n'ayant aucun point fixe comme le cardinal d'une réunion d'ensembles finis (en t'aidant de la question précédente).
- Enfin calcule ce nombre (Indice: Principe d'inclusion-exclusion)
- Là, il te reste plus grand chose à faire pour calculer ta proba :lol3:
Une des (multiples) autres façons, c'est de dire que, si on note dn le nombre de dérangement, toute les permutations de {1..n} s'obtiennent (de façon unique) en choisissant j dans {0..n} puis une partie J de {1..n} à j élément sur laquelle la permutation sera l'identité puis un dérangement sur le complémentaire {1..n}\J.
Ca nous dit donc que, pour tout n,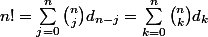 qui est un système linéaire (si on se limite à
qui est un système linéaire (si on se limite à 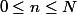 avec N fixé)
avec N fixé)
Or, la matrice des coeffs_{0\leq n,k\leq N}) a pour inverse
a pour inverse ^k{n\choose k})_{0\leq n,k\leq N}) donc, pour tout n,
donc, pour tout n, ^k{n\choose k}k!)
Edit : évidement, il faut connaitre l'inverse de la matrice formé du triangle de pascal, mais
a) C'est un "très grand classique" en dénombrement
b) Le résultat est totalement trivial une fois qu'on a vu que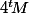 est, par définition, la matrice dans la base canonique de l'application linéaire
est, par définition, la matrice dans la base canonique de l'application linéaire \mapsto P(X+1)) dont l'inverse est évidement
dont l'inverse est évidement \mapsto P(X-1))
Ca nous dit donc que, pour tout n,
Or, la matrice des coeffs
Edit : évidement, il faut connaitre l'inverse de la matrice formé du triangle de pascal, mais
a) C'est un "très grand classique" en dénombrement
b) Le résultat est totalement trivial une fois qu'on a vu que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Autre méthode axée sur le fait qu'un un dérangement de {1..n}, c'est une permutation qui se décompose en cycles à supports disjoints de longueur au moins égal à 2.
Donc ça s'écrit de façon unique comme un cycle de longueur k>=1 commençant par 1 composé avec un dérangement des n-k autres éléments ce qui nous dit que, pour tout ,
,
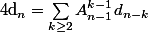
Donc ça s'écrit de façon unique comme un cycle de longueur k>=1 commençant par 1 composé avec un dérangement des n-k autres éléments ce qui nous dit que, pour tout
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
